题目内容
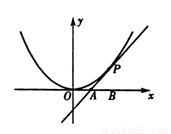
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,点B的坐标为(2,0),(1)若动点M满足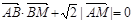 ,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.
,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.
【答案】
(I)动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为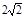 ,短轴长为2的椭圆;(II)△OBE与△OBF面积之比的取值范围是(3-2
,短轴长为2的椭圆;(II)△OBE与△OBF面积之比的取值范围是(3-2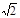 ,1).
,1).
【解析】根据导数的几何意义,可以得出直线的方程,从而得出A坐标,再设设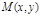 带入已知条件得出x,y的关系式;直线与椭圆的关系通常联立直线与椭圆方程得出关于x的一元二次方程,
带入已知条件得出x,y的关系式;直线与椭圆的关系通常联立直线与椭圆方程得出关于x的一元二次方程,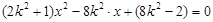 ,结合韦达定理,
,结合韦达定理,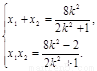
表达出△OBE与△OBF面积之比的代数式。
解:(I)由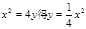 ,
,
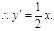
∴直线l的斜率为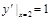 ,故l的方程为
,故l的方程为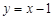 ,
,
∴点A坐标为(1,0)设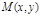 则
则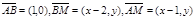 ,
,
由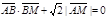 得
得
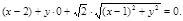 整理,得
整理,得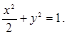
∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为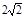 ,短轴长为2的椭圆
,短轴长为2的椭圆
(II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
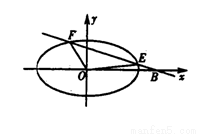
将①代入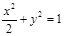 ,整理,得
,整理,得
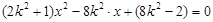 ,
,
由△>0得0<k2<0.5. 设E(x1,y1),F(x2,y2)
则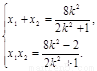 ② 令
② 令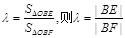 ,
,
由此可得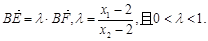 由②知
由②知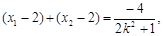
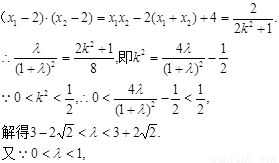
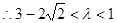 .
.
∴△OBE与△OBF面积之比的取值范围是(3-2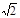 ,1)
,1)

练习册系列答案
相关题目
 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).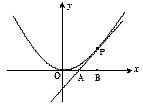 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
