题目内容
已知两单位向量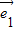 ,
,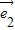 的夹角为60°,则向量
的夹角为60°,则向量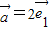 +
+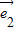 与
与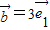 -2
-2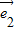 的夹角为 .?
的夹角为 .?
【答案】分析:由条件求得|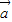 |、|
|、|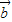 |、以及
|、以及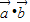 的值,设向量
的值,设向量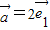 +
+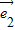 与
与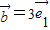 -2
-2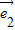 的夹角为θ,则 0≤θ≤π,利用两个向量的夹角公式cosθ=
的夹角为θ,则 0≤θ≤π,利用两个向量的夹角公式cosθ=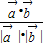 ,运算求得结果.
,运算求得结果.
解答:解:∵单位向量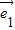 ,
,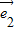 的夹角为60°,∴|
的夹角为60°,∴|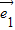 |=|
|=|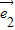 |=1,且
|=1,且 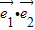 =1×1cos60°=
=1×1cos60°= .
.
∴|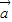 |=
|=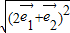 =
=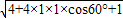 =
=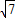 ,
,
|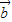 |=
|=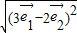 =
=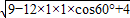 =
=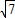 ,
,
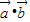 =(2
=(2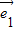 +
+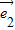 )•(3
)•(3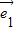 -2
-2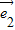 )=6
)=6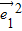 -
-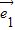 •
•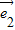 -2
-2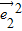 =6-
=6- -2=
-2= .
.
设向量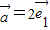 +
+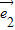 与
与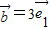 -2
-2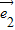 的夹角为θ,则 0≤θ≤π,
的夹角为θ,则 0≤θ≤π,
cosθ=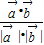 =
=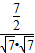 =
= ,∴θ=
,∴θ=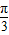 ,
,
故答案为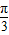 .
.
点评:本题主要考查两个向量的夹角公式的应用,求向量的模的方法,根据三角函数的值求角,属于中档题.
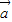 |、|
|、|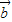 |、以及
|、以及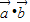 的值,设向量
的值,设向量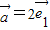 +
+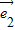 与
与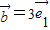 -2
-2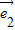 的夹角为θ,则 0≤θ≤π,利用两个向量的夹角公式cosθ=
的夹角为θ,则 0≤θ≤π,利用两个向量的夹角公式cosθ=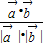 ,运算求得结果.
,运算求得结果.解答:解:∵单位向量
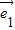 ,
,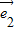 的夹角为60°,∴|
的夹角为60°,∴|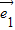 |=|
|=|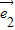 |=1,且
|=1,且 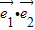 =1×1cos60°=
=1×1cos60°= .
.∴|
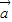 |=
|=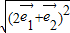 =
=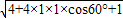 =
=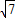 ,
,|
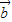 |=
|=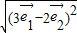 =
=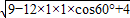 =
=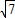 ,
,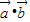 =(2
=(2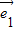 +
+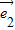 )•(3
)•(3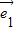 -2
-2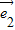 )=6
)=6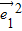 -
-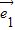 •
•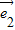 -2
-2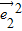 =6-
=6- -2=
-2= .
.设向量
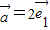 +
+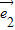 与
与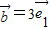 -2
-2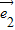 的夹角为θ,则 0≤θ≤π,
的夹角为θ,则 0≤θ≤π,cosθ=
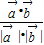 =
=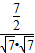 =
= ,∴θ=
,∴θ=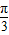 ,
,故答案为
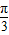 .
.点评:本题主要考查两个向量的夹角公式的应用,求向量的模的方法,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
 与
与 的夹角为
的夹角为 ,若
,若 ,
, ,试求
,试求 与
与 的夹角
的夹角 。
。 ,
, 的夹角为60°,则向量
的夹角为60°,则向量 +
+ 与
与 -2
-2 的夹角为 .?
的夹角为 .? 与
与 的夹角为120°,若
的夹角为120°,若 ,
, ,试求
,试求 与
与 的夹角θ.
的夹角θ. ,
, 的夹角为60°,则两向量
的夹角为60°,则两向量 =2
=2 +
+ 与
与 =-3
=-3 +2
+2 的夹角为( )
的夹角为( ) 与
与 的夹角为
的夹角为 ,且
,且
 与
与
 与
与 的夹角
的夹角