题目内容
求证:(sin2x+
证明:∵(a-b)2=a2+b2-2ab≥0,
∴a2+b2≥2ab,
若ab≥0,则ab=![]() ≤
≤![]() 结合
结合
sin2x+cos2x=1,
∴![]() ≤
≤![]() =
=![]() .
.
∴sin2x·cos2x≤![]() .
.
∴1-sin2x·cos2x≥![]() .
.
∴(sin2x+![]() )(cos2x+
)(cos2x+![]() )
)
=![]() ·
·![]()
=![]()
=![]()
=![]()
≥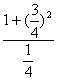 =
=![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
题目内容
求证:(sin2x+
证明:∵(a-b)2=a2+b2-2ab≥0,
∴a2+b2≥2ab,
若ab≥0,则ab=![]() ≤
≤![]() 结合
结合
sin2x+cos2x=1,
∴![]() ≤
≤![]() =
=![]() .
.
∴sin2x·cos2x≤![]() .
.
∴1-sin2x·cos2x≥![]() .
.
∴(sin2x+![]() )(cos2x+
)(cos2x+![]() )
)
=![]() ·
·![]()
=![]()
=![]()
=![]()
≥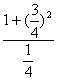 =
=![]() .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案