题目内容
如图, 是以
是以 为直径的
为直径的 上一点,
上一点, 于点
于点 ,过点
,过点 作
作 的切线,与
的切线,与 的延长线相交于点
的延长线相交于点 是
是 的中点,连结
的中点,连结 并延长与
并延长与 相交于点
相交于点 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点 .
.

(1)求证: ;
;
(2)求证: 是
是 的切线;
的切线;
(3)若 ,且
,且 的半径长为
的半径长为 ,求
,求 和
和 的长度.
的长度.
【答案】
(1)根据三角形 的相似来证明,
的相似来证明,
(2)要证明直线是圆的切线,只要证明圆心与切点的连线与直线垂直即可。
(3) ,
,
【解析】
试题分析:.(1)证明: 是
是 的直径,
的直径, 是
是 的切线,
的切线,
 .又
.又 ,
, .
.
易证 ,
, .
.
 .
. .
.
 是
是 的中点,
的中点, .
. .
.
(2)证明:连结 .
. 是
是 的直径,
的直径, .
.
在 中,由(1),知
中,由(1),知 是斜边
是斜边 的中点,
的中点,
 .
. .又
.又 ,
, .
.
 是
是 的切线,
的切线, .
.
 ,
, 是
是 的切线.
的切线.
(3)解:过点 作
作 于点
于点 .
. ,
, .
.
由(1),知 ,
, .
.
由已知,有 ,
, ,即
,即 是等腰三角形.
是等腰三角形.
 ,
, .
. ,
, ,即
,即 .
.
 ,
, 四边形
四边形 是矩形,
是矩形, .
.
 ,易证
,易证 .
. ,即
,即 .
.
 的半径长为
的半径长为 ,
, .
. .
.
解得 .
. .
. ,
, .
. .
.
在 中,
中, ,
, ,由勾股定理,得
,由勾股定理,得 .
.
 .解得
.解得 (负值舍去).
(负值舍去). .
.
[或取 的中点
的中点 ,连结
,连结 ,则
,则 .易证
.易证 ,
, ,故
,故 ,
, .由
.由 ,易知
,易知 ,
, .
.
由 ,解得
,解得 .又在
.又在 中,由勾股定理,得
中,由勾股定理,得
 ,
, (舍去负值).]
(舍去负值).]

考点:三角形的相似,圆 的性质
点评:主要是考查了圆内的性质以及相似三角形的性质的运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是以
是以 为直径的半圆
为直径的半圆 上的一点,过
上的一点,过 ,交过A点的切线于
,交过A点的切线于 ,
, .
.
 是圆
是圆 ,求
,求 .
.  是以
是以 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且

 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 ,
, //
// ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 是以
是以 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形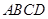 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且

 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 ,
, //
// ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
. ;
;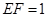 ,求三棱锥
,求三棱锥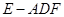 的体积.
的体积.