题目内容
(本小题满分12分)
如图, 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且 .
.

(Ⅰ)求证: ;
;
(Ⅱ)设平面 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
.
①试证: ;
;
②若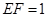 ,求三棱锥
,求三棱锥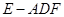 的体积.
的体积.
【答案】
(1)通过证明 面
面 ,进而得到线线垂直的证明。
,进而得到线线垂直的证明。
(2)利用 平面
平面 的性质定理,可知线线平行,体积为
的性质定理,可知线线平行,体积为
【解析】
试题分析:解:(Ⅰ)∵平面
 平面
平面 ,
,
面
 面
面
 ,
, ,
, 面
面 ,
,
∴ 面
面 . ………………………… 2分
. ………………………… 2分
又∵ 面
面 ,∴
,∴ . …………………………
3分
. …………………………
3分
∵ 在以
在以 为直径的半圆上,∴
为直径的半圆上,∴ ,
,
又∵ ,
, 面
面 ,∴
,∴ 面
面 .…………… 4分
.…………… 4分
又∵ 面
面 ,∴
,∴ . ………………………
5分
. ………………………
5分
(Ⅱ)① ∵ ,
, 面
面 ,
, 面
面 ,
,
∴ 平面
平面 .… 6分
.… 6分
又∵ 面
面 ,平面
,平面 平面
平面
 ,
,
∴ . ……………… 8分
. ……………… 8分
②取 中点
中点 ,
, 的中点
的中点 ,
,
在 中,
中, ,
, ,∴
,∴ .
.
(Ⅰ)已证得 面
面 ,又已知
,又已知 ,
,
∴ 平面
平面 .…………… 10分
.…………… 10分
故
 . … 12分
. … 12分
考点:线线垂直,线线平行,体积运算知识。
点评:本小题主要考查直线与直线、直线与平面的位置关系及棱锥体积等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想等,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目