题目内容
如图, 是以
是以 为直径的半圆
为直径的半圆 上的一点,过
上的一点,过 的直线交直线
的直线交直线 于
于 ,交过A点的切线于
,交过A点的切线于 ,
, .
.

(Ⅰ)求证: 是圆
是圆 的切线;
的切线;
(Ⅱ)如果 ,求
,求 .
.
【答案】
(Ⅰ)见解析;(Ⅱ)  .
.
【解析】
试题分析:(Ⅰ) 连接 ,
, ,根据直径所对的圆心角是直角可知,
,根据直径所对的圆心角是直角可知, ,结合已知条件“
,结合已知条件“ ”得,
”得, ,所以
,所以 是
是 的中垂线,由中垂线的性质可得到,
的中垂线,由中垂线的性质可得到, ,
, ,把角
,把角 转化为
转化为 ,即可得到
,即可得到 ,则结论可证;(Ⅱ)先根据两个对应角相等得到
,则结论可证;(Ⅱ)先根据两个对应角相等得到 ,由相似三角形对应线段成比例求出线段
,由相似三角形对应线段成比例求出线段 的值,进一步求出
的值,进一步求出 的值,由平行线分线段成比例可得到
的值,由平行线分线段成比例可得到 的值,从而解出
的值,从而解出 .
.
试题解析:(Ⅰ)连接 ,
, ,
,

 是直径,则
是直径,则 .
.
由 得,
得, ,
,
则 是
是 的中垂线,
的中垂线,
所以 ,
, ,
,
所以 ,
,
则 ,即
,即 是圆
是圆 的切线.
5分
的切线.
5分
(Ⅱ)因为 ,
,
所以 ,
, ,
,
则有 ,
,
所以 ,那么
,那么 ,
,
所以 ,
,
所以 ,
,
所以 ,
,
解得 .
10分
.
10分
考点:1.三角形相似的判定及其性质;2.平行线分线段成比例;3.切线的性质及判定

练习册系列答案
相关题目
 是以
是以 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且

 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 ,
, //
// ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 是以
是以 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形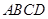 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且

 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 ,
, //
// ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
. ;
;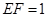 ,求三棱锥
,求三棱锥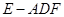 的体积.
的体积. 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.