题目内容
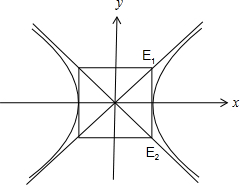 如图所示,直线x=2与双曲线Γ:
如图所示,直线x=2与双曲线Γ:| x2 |
| 4 |
| OE1 |
| e1 |
| OE2 |
| e2 |
| OP |
| e1 |
| e2 |
分析:先根据双曲线的方程可得渐近线,进而可得E1,E2两点坐标,根据
=a
+b
,求得
代入双曲线方程,即可求得a和b的关系.
| OP |
| e1 |
| e2 |
| OP |
解答:解:依题意可知:E1(2,1),E2(2,-1)
∴
=a
+b
=(2a+2b,a-b),
∵点P在双曲线上
∴
-(a-b)2=1,
化简得4ab=1
故答案为4ab=1
∴
| OP |
| e1 |
| e2 |
∵点P在双曲线上
∴
| (2a+2b)2 |
| 4 |
化简得4ab=1
故答案为4ab=1
点评:本题主要考查了双曲线的简单性质.属基础题.

练习册系列答案
相关题目
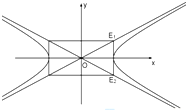 如图所示,直线x=2与双曲线C:
如图所示,直线x=2与双曲线C:

 的渐近线交于
的渐近线交于 ,
, 两点,记
两点,记 ,任取双曲线
,任取双曲线 上的点P,若
上的点P,若 ,则a、b满足的一个等式是
,则a、b满足的一个等式是