题目内容
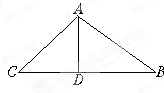
如图，在△ABC中，AB=4cm，AC=3cm，角平分线AD=2cm，求此三角形面积．
考点：正弦定理
专题：解三角形
分析：设∠CAD=∠BAD=θ，由于AD是∠CAB的角平分线，可得
=
=
．设CD=3x，则DB=4x．在△ACD与△ADB中，分别利用余弦定理可得：
=
．解得x2．再利用同角三角函数基本关系式和倍角公式可得sin2θ，利用三角形的面积计算公式即可得出．．
| CD |
| DB |
| AC |
| AB |
| 3 |
| 4 |
| 13-9x2 |
| 12 |
| 5-4x2 |
| 4 |
解答：
解：设∠CAD=∠BAD=θ，∵AD是∠CAB的角平分线，∴
=
=
．
设CD=3x，则DB=4x．
在△ACD与△ADB中，分别利用余弦定理可得：
cosθ=
=
，cosθ=
=
．
∴
=
．
解得x2=
．
∴cosθ=
，∴sinθ=
=
．
sin2θ=2×
×
=
．
∴此三角形面积S=
×4×3×
=
．
| CD |
| DB |
| AC |
| AB |
| 3 |
| 4 |
设CD=3x，则DB=4x．
在△ACD与△ADB中，分别利用余弦定理可得：
cosθ=
| 32+22-(3x)2 |
| 2×3×2 |
| 13-9x2 |
| 12 |
| 42+22-(4x)2 |
| 2×4×2 |
| 5-4x2 |
| 4 |
∴
| 13-9x2 |
| 12 |
| 5-4x2 |
| 4 |
解得x2=
| 2 |
| 3 |
∴cosθ=
| 7 |
| 12 |
| 1-cos2θ |
| ||
| 12 |
sin2θ=2×
| 7 |
| 12 |
| ||
| 12 |
7
| ||
| 72 |
∴此三角形面积S=
| 1 |
| 2 |
7
| ||
| 72 |
7
| ||
| 12 |
点评：本题综合考查了角平分线的性质、余弦定理、同角三角函数基本关系式和倍角公式、三角形的面积计算公式，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
已知函数f（x）=ax+b的图象如图所示．