题目内容
袋中装有黑球和白球共7个,从中任取两个球都是白球的概率为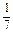 .现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求取球2次终止的概率;
(3)求甲取到白球的概率.
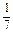 .现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.(1)求袋中原有白球的个数;
(2)求取球2次终止的概率;
(3)求甲取到白球的概率.
(1)3(2) (3)
(3)
 (3)
(3)
(1)设袋中有n个白球,从袋中任取2个球是白球的结果数是 .
.
从袋中任取2个球的所有可能的结果数为 =21.
=21.
由题意知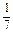 =
= =
= ,
,
∴n(n-1)=6,解得n=3(舍去n=-2).
故袋中原有3个白球.
(2)记“取球2次终止”为事件A,则P(A)= =
= .
.
(3)记“甲取到白球”的事件为B,
“第i次取到白球”为Ai,i=1,2,3,4,5,
因为甲先取,所以甲只有可能在第1次,第3次和第5次取球.
所以P(B)=P(A1+A3+A5).
因此A1,A3,A5两两互斥,
∴P(B)=P(A1)+P(A3)+P(A5)
= +
+ +
+
= +
+ +
+ =
= .
.
 .
.从袋中任取2个球的所有可能的结果数为
 =21.
=21.由题意知
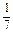 =
= =
= ,
,∴n(n-1)=6,解得n=3(舍去n=-2).
故袋中原有3个白球.
(2)记“取球2次终止”为事件A,则P(A)=
 =
= .
.(3)记“甲取到白球”的事件为B,
“第i次取到白球”为Ai,i=1,2,3,4,5,
因为甲先取,所以甲只有可能在第1次,第3次和第5次取球.
所以P(B)=P(A1+A3+A5).
因此A1,A3,A5两两互斥,
∴P(B)=P(A1)+P(A3)+P(A5)
=
 +
+ +
+
=
 +
+ +
+ =
= .
.
练习册系列答案
相关题目
 本,英文书
本,英文书 本,日文书
本,日文书 本,则抽出一本书为外文书的概率为()
本,则抽出一本书为外文书的概率为()



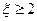 ,则该同学就迟到,求该同学不迟到的概率;
,则该同学就迟到,求该同学不迟到的概率;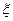 的数学期望和方差
的数学期望和方差




 ,
, ;
; 为一次函数的概率;
为一次函数的概率; 为二次函数的概率。
为二次函数的概率。 ,则以
,则以 为坐标的点落在第四象限的
为坐标的点落在第四象限的