题目内容
15.已知A={1,2,x},B={1,x2},且A∩B=B,求x的值.分析 根据A∩B=B便可得到B⊆A,从而有x2=2,或x2=x,可以求出x,然后将x带回集合A,B,便可判断是否满足集合元素的互异性,从而得出x的值.
解答 解:∵A∩B=B;
∴B⊆A;
∴x2=2,或x2=x;
即$x=±\sqrt{2}$,或x=0,或x=1;
将x值代入集合A,B得:
∴$x=±\sqrt{2}$,或x=0满足集合元素的互异性,并满足A∩B=B;
而x=1时,不满足集合元素的互异性;
故$x=±\sqrt{2}$,或x=0.
点评 考查列举法表示集合,交集的概念及子集的定义,元素与集合的关系,在求出x后要验证是否满足集合元素的互异性.

练习册系列答案
相关题目
10.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ex | B. | y=cosx | C. | y=|x|+1 | D. | y=$\sqrt{x}$ |
20.函数y=$\frac{x+2}{x-1}$(x≠1)在区间[2,5)上的最大值、最小值分别是( )
| A. | $\frac{7}{4}$,4 | B. | 无最大值,最小值7 | ||
| C. | 4,0 | D. | 最大值4,无最小值 |
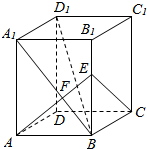 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.