题目内容
5.已知二次函数的图象过点(-3,0),(1,0),且顶点到x轴的距离等于2,则此二次函数的表达式为y=$\frac{1}{2}{x^2}+x-\frac{3}{2}$,或y=-$\frac{1}{2}{x^2}-x+\frac{3}{2}$.分析 法一:设函数为交点式,利用二次函数图象的顶点到x轴的距离2,可得函数解析式;
法二:设函数为顶点式,利用函数图象过点(1,0),可得函数解析式.
解答 解:法一:∵二次函数的图象过点(-3,0),(1,0),
∴可设二次函数为y=a(x+3)(x-1)(a≠0),
展开,得 y=ax2+2ax-3a,
顶点的纵坐标为 $\frac{{-12{a^2}-4{a^2}}}{4a}=-4a$,
由于二次函数图象的顶点到x轴的距离2,
∴|-4a|=2,即a=$±\frac{1}{2}$.
所以,二次函数的表达式为y=$\frac{1}{2}{x^2}+x-\frac{3}{2}$,或y=-$\frac{1}{2}{x^2}-x+\frac{3}{2}$.
法二:∵二次函数的图象过点(-3,0),(1,0),
∴对称轴为直线x=-1.
又顶点到x轴的距离为2,
∴顶点的纵坐标为2,或-2.
于是可设二次函数为y=a(x+1)2+2,或y=a(x+1)2-2,
由于函数图象过点(1,0),
∴0=a(1+1)2+2,或0=a(1+1)2-2.
∴a=-$\frac{1}{2}$,或a=$\frac{1}{2}$.
所以,所求的二次函数为y=-$\frac{1}{2}$(x+1)2+2,或y=$\frac{1}{2}$(x+1)2-2.
故答案为:y=$\frac{1}{2}{x^2}+x-\frac{3}{2}$,或y=-$\frac{1}{2}{x^2}-x+\frac{3}{2}$.
点评 本题考查函数解析式的求法,解题的关键是正确设出函数的解析式,利用待定系数法是解决本题的关键..

练习册系列答案
相关题目
13.已知F1,F2分别是双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点,O为坐标原点,P为双曲线右支上的一点,PF1与以F2为圆心,|OF2|为半径的圆相切于点Q,且Q恰好是PF1的中点,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{5}-1$ |
10.已知函数f(x)=$\left\{\begin{array}{l}{2+|x-2|,}&{x≥0}\\{{x}^{2}}&{x<0}\end{array}\right.$,当函数g(x)=k-f(x)有三个零点时,实数k的取值范围是( )
| A. | <k<2 | B. | k≥2 | C. | 2<k≤4 | D. | 2≤k≤4 |
14.已知a,b∈R+,函数f(x)=alog2x+b的图象经过点(4,1),则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 6-2$\sqrt{2}$ | B. | 6 | C. | 4+2$\sqrt{2}$ | D. | 8 |
 如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.
如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.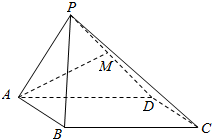 如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,其中,四边形ABCD为正方形,△PAD是正三角形,M是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,其中,四边形ABCD为正方形,△PAD是正三角形,M是PD的中点.