题目内容
“ ”是“函数
”是“函数 在区间
在区间 上为增函数”的
上为增函数”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:根据绝对值函数可知,函数 在区间
在区间 上为增函数,那么说明了a
上为增函数,那么说明了a ,而条件是
,而条件是 ,可知条件的集合小于结论的集合,故可知条件是结论成立的充分不必要条件,选A.
,可知条件的集合小于结论的集合,故可知条件是结论成立的充分不必要条件,选A.
考点:充分条件
点评:解决的关键是对于函数的单调性的理解和准确的表示,属于基础题。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
不等式 的解集记为
的解集记为 ,关于
,关于 的不等式
的不等式 的解集记为
的解集记为 ,若
,若 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
下列说法中,正确的是( )
A.命题“若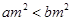 ,则 ,则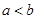 ”的逆命题是真命题 ”的逆命题是真命题 |
B.已知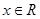 ,则“ ,则“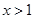 ”是“ ”是“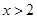 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“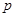 或 或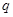 ”为真命题,则命题“ ”为真命题,则命题“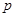 ”和命题“ ”和命题“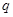 ”均为真命题 ”均为真命题 |
D.命题“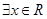 , ,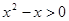 ”的否定是:“ ”的否定是:“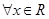 , ,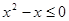 ” ” |
设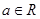 ,则“
,则“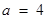 ”是“直线
”是“直线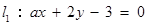 与直线
与直线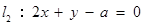 平行”的( )
平行”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“直线
”是“直线 与直线
与直线 垂直”的( )
垂直”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
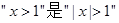 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
“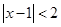 成立”是“
成立”是“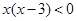 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
某个命题与正整数n有关,如果当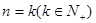 时命题成立,那么可推得当
时命题成立,那么可推得当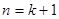 时命题也成立. 现已知当
时命题也成立. 现已知当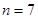 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
| A.当n=6时该命题不成立 | B.当n=6时该命题成立 |
| C.当n=8时该命题不成立 | D.当n=8时该命题成立 |
“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |