题目内容
下列说法中,正确的是( )
A.命题“若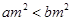 ,则 ,则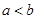 ”的逆命题是真命题 ”的逆命题是真命题 |
B.已知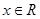 ,则“ ,则“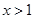 ”是“ ”是“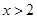 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“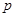 或 或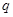 ”为真命题,则命题“ ”为真命题,则命题“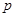 ”和命题“ ”和命题“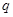 ”均为真命题 ”均为真命题 |
D.命题“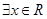 , ,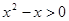 ”的否定是:“ ”的否定是:“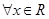 , ,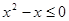 ” ” |
D
解析试题分析:A.命题“若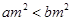 ,则
,则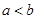 ”的逆命题是真命题,错误,因为,
”的逆命题是真命题,错误,因为, =0时不成立;
=0时不成立;
B.已知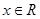 ,则“
,则“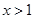 ”是“
”是“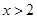 ”的充分不必要条件,错误,因为,
”的充分不必要条件,错误,因为,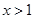 时,不能推出
时,不能推出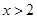 ;
;
C.命题“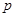 或
或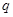 ”为真命题,则命题“
”为真命题,则命题“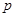 ”和命题“
”和命题“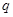 ”均为真命题,错误,因为,由真值表可知,命题“
”均为真命题,错误,因为,由真值表可知,命题“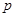 或
或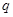 ”为真命题,p,q至少有一个为真命题;
”为真命题,p,q至少有一个为真命题;
D.命题“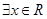 ,
,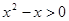 ”的否定是:“
”的否定是:“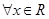 ,
,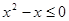 ”,是真命题,因为,存在性命题的否定是全称命题;故选D。
”,是真命题,因为,存在性命题的否定是全称命题;故选D。
考点:充要条件,命题,复合命题,不等式的性质。
点评:小综合题,本题综合性较强,考查知识较多。需综合运用数学知识加以解答。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列命题:
(1)“若 ,则
,则 互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;
互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;
(3)“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
(4)“若
 ,则
,则 ”的逆否命题.
”的逆否命题.
其中为真命题的是( )
| A.(1)(2) | B.(2)(3) | C.(1)(2)(3) | D.(3)(4) |
下列说法正确的是( )
A.函数 在其定义域上是减函数 在其定义域上是减函数 |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.命题“ R, R, ”的否定是“ ”的否定是“  R, R, ” ” |
D.给定命题 、 、 ,若 ,若 是真命题,则 是真命题,则 是假命题 是假命题 |
下列命题是真命题的是 ( )
A. 是 是 的充要条件 的充要条件 | B. , , 是 是 的充分条件 的充分条件 |
C. , , > > | D. , , < 0 < 0 |
“ ” 是“直线
” 是“直线 与直线
与直线 平行” 的( )
平行” 的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数 ,
, ,则函数
,则函数 在
在 上递增是
上递增是 在
在 上递增的( )
上递增的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
“ ”是“函数
”是“函数 在区间
在区间 上为增函数”的
上为增函数”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知p:“x2+ y2 +2x=F为一圆的方程(F∈R)”,q:“F>0”,则p是q的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
 为真命题,则
为真命题,则 为真命题.
为真命题. 的充分不必要条件是
的充分不必要条件是 .
. ,使得
,使得 ,则
,则 .
. ,则
,则 或
或 "的逆否命题为"若
"的逆否命题为"若 或
或 ,则
,则 ".
".