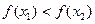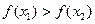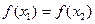题目内容
(本题满分14分)函数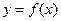 对任意实数
对任意实数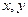 都有
都有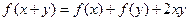 .
.
(1)若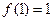 ,求
,求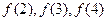 的值;
的值;
(2)对于任意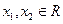 ,求证:
,求证: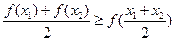 ;
;
(3)若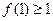 ,求证:
,求证: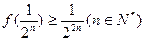 .
.
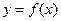 对任意实数
对任意实数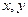 都有
都有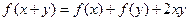 .
.(1)若
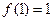 ,求
,求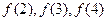 的值;
的值;(2)对于任意
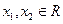 ,求证:
,求证: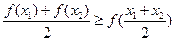 ;
;(3)若
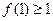 ,求证:
,求证: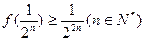 .
.(1)由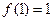 及
及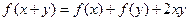 ,可得
,可得
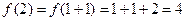 ,
,
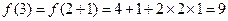 ,
,
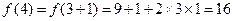 . …………3分
. …………3分
(2)证明: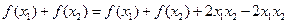 …………4分
…………4分
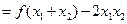 …………5分
…………5分
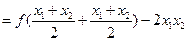
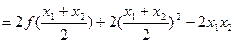 …………6分
…………6分
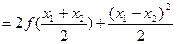 …………7分
…………7分
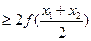 . …………8分
. …………8分
所以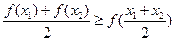 . …………9分
. …………9分
(若直接由某一具体函数(如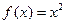 )得出证明,整个第2小题只给2分)
)得出证明,整个第2小题只给2分)
(3)①因为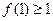 ,所以
,所以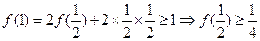
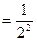 ,即
,即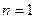 时,原不等式成立. ………10分
时,原不等式成立. ………10分
②假设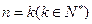 时不等式成立,即
时不等式成立,即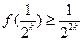 ,则
,则
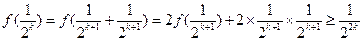 ,
,
所以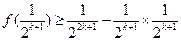 ,
,
即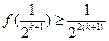 ,
,
即当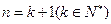 时原不等式也成立. …………13分
时原不等式也成立. …………13分
由①②知,当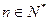 时,都有
时,都有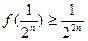 成立. …………14分
成立. …………14分
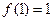 及
及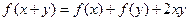 ,可得
,可得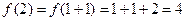 ,
,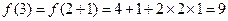 ,
,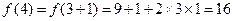 . …………3分
. …………3分(2)证明:
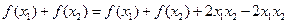 …………4分
…………4分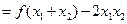 …………5分
…………5分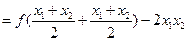
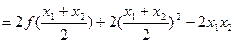 …………6分
…………6分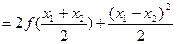 …………7分
…………7分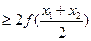 . …………8分
. …………8分所以
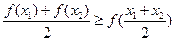 . …………9分
. …………9分(若直接由某一具体函数(如
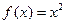 )得出证明,整个第2小题只给2分)
)得出证明,整个第2小题只给2分)(3)①因为
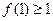 ,所以
,所以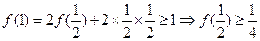
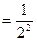 ,即
,即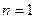 时,原不等式成立. ………10分
时,原不等式成立. ………10分②假设
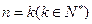 时不等式成立,即
时不等式成立,即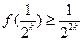 ,则
,则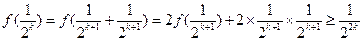 ,
,所以
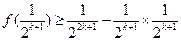 ,
,即
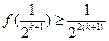 ,
,即当
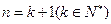 时原不等式也成立. …………13分
时原不等式也成立. …………13分由①②知,当
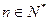 时,都有
时,都有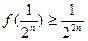 成立. …………14分
成立. …………14分略

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
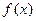 的定义域为
的定义域为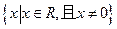 对定义域内的任意
对定义域内的任意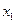 、
、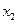 ,都有
,都有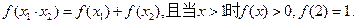
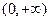 上是增函数;
上是增函数;
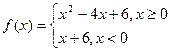 则不等式
则不等式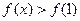 的解集是( )
的解集是( )



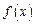 满足:对任意实数
满足:对任意实数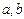 都有
都有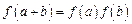 ,且
,且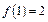 ,
,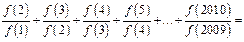 _____________________.
_____________________.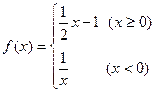 ,则f[f(1)]=
,则f[f(1)]=  若
若 则
则 的范围是( )
的范围是( )



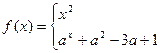
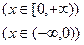 在区间
在区间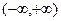 是增函数,则常数a的取值范围是
是增函数,则常数a的取值范围是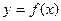 ,满足
,满足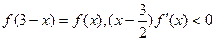 ,若
,若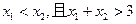 则有 ( )
则有 ( )