题目内容
已知函数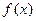 的定义域为
的定义域为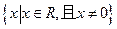 对定义域内的任意
对定义域内的任意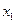 、
、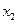 ,都有
,都有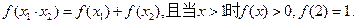
(1)求证: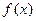 是偶函数;
是偶函数;
(2)求证: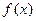 在
在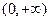 上是增函数;
上是增函数;
(3)解不等式
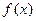 的定义域为
的定义域为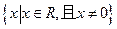 对定义域内的任意
对定义域内的任意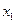 、
、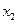 ,都有
,都有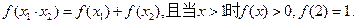
(1)求证:
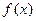 是偶函数;
是偶函数;(2)求证:
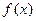 在
在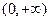 上是增函数;
上是增函数;(3)解不等式

(1),(2)证明略,(3)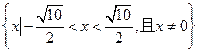
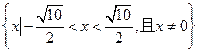
证明抽象函数的单调性通常是用单调性的定义结合比较法.
(1)证明 因对定义域内的任意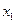 、
、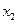 都有
都有
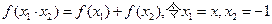 ,则有
,则有
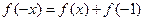 ……2分
……2分
又令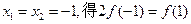
再令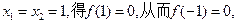
于是有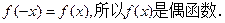
(2)设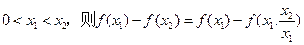
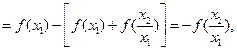
由于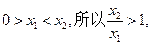 从而
从而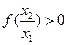 ,
,
故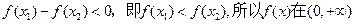 上是增函数. (3)由于
上是增函数. (3)由于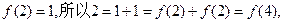
于是待解不等式可化为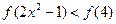 , 结合(1)(2)已证结论,可得上式等价于
, 结合(1)(2)已证结论,可得上式等价于 
解得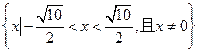 .
.
【名师指引】作差法、作商法以及函数的单调性是比较大小的常用方法.运用不等式性质时应从结论出发, 寻找解题的切入点.
(1)证明 因对定义域内的任意
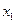 、
、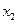 都有
都有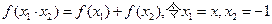 ,则有
,则有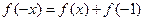 ……2分
……2分又令
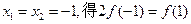
再令
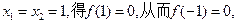
于是有
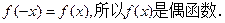
(2)设
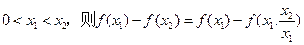
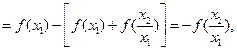
由于
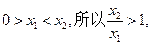 从而
从而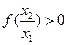 ,
, 故
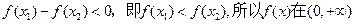 上是增函数. (3)由于
上是增函数. (3)由于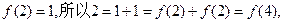
于是待解不等式可化为
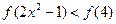 , 结合(1)(2)已证结论,可得上式等价于
, 结合(1)(2)已证结论,可得上式等价于 
解得
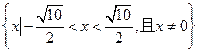 .
. 【名师指引】作差法、作商法以及函数的单调性是比较大小的常用方法.运用不等式性质时应从结论出发, 寻找解题的切入点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与销售数量
与销售数量 的函数关系式;
的函数关系式;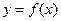 对任意实数
对任意实数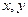 都有
都有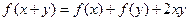 .
.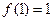 ,求
,求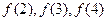 的值;
的值;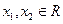 ,求证:
,求证: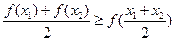 ;
;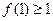 ,求证:
,求证: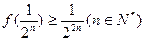 .
. –(2a)2]对任意x∈[
–(2a)2]对任意x∈[ ,+∞]都有意义,则实数a的取值范围是( )
,+∞]都有意义,则实数a的取值范围是( )


 )
)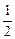 )
)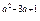 的单调递减区间.
的单调递减区间. ,则
,则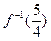 =
=