题目内容
(本题满分15分)已知 ,
,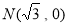 是平面上的两个定点,动点
是平面上的两个定点,动点 满足
满足 .
.
(1)求动点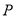 的轨迹方程;
的轨迹方程;
(2)已知圆方程为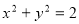 ,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于
,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于 ,
,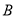 两点,
两点,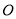 为坐标原点,设
为坐标原点,设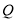 为
为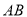 的中点,求
的中点,求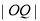 长度的取值范围.
长度的取值范围.
(1) ;(2)
;(2)
【解析】
试题分析:(1)根据椭圆定义知点 的轨迹为焦点在
的轨迹为焦点在 轴上的椭圆且
轴上的椭圆且 ,
, ,
, ,
,
故动点 的轨迹方程为
的轨迹方程为 ;(2)若直线
;(2)若直线 斜率不存在,则直线
斜率不存在,则直线 方程为
方程为 ,
,
则 ,若直线
,若直线 斜率存在,设直线
斜率存在,设直线 方程为
方程为 ,由
,由

 ,又直线
,又直线 与圆
与圆 相切,则
相切,则
 ,所以
,所以 再对k进行分类讨论即可求得
再对k进行分类讨论即可求得 长度的取值范围
长度的取值范围
试题解析:(1)由题意知,点 的轨迹为焦点在
的轨迹为焦点在 轴上的椭圆, 2分
轴上的椭圆, 2分
且 ,
, ,
, ,
,
∴动点 的轨迹方程为
的轨迹方程为 5分
5分
(2)若直线 斜率不存在,则直线
斜率不存在,则直线 方程为
方程为 ,
,
此时, 6分
6分
若直线 斜率存在,设直线
斜率存在,设直线 方程为
方程为 ,
, ,
,
联立 ,得:
,得:
∴
 8分
8分
∴ ∴
∴ 9分
9分
∵直线 与圆
与圆 相切,∴
相切,∴ ,即
,即 11分
11分
∴
当 时,
时,
当 时,
时, , 14分
, 14分
当且仅当 时,等号成立 ∴
时,等号成立 ∴ 15分
15分
考点:圆锥曲线的综合应用

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 上随机选取一个数
上随机选取一个数 ,则
,则 的概率为( )
的概率为( )



 为实数,则方程
为实数,则方程 至少有一个实根”时,要做的假设是
至少有一个实根”时,要做的假设是 ,已知
,已知 ,
, ,
, ,则边a=__________;△ABC的面积等于 .
,则边a=__________;△ABC的面积等于 . ,
, 是椭圆的两个焦点,若椭圆上存在点P,使得
是椭圆的两个焦点,若椭圆上存在点P,使得 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( ) B.
B. C.
C. D.
D.
 的解集是区间
的解集是区间 的子集,
的子集, 的范围为 .
的范围为 . ,
, 是双曲线
是双曲线
 ,
, 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点 ,使
,使 (
( 为坐标原点),且
为坐标原点),且 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( ) B.
B. C.
C. D.
D.
 和识图能力
和识图能力 进行统计分析,得到如下数据:
进行统计分析,得到如下数据:

 若某儿童的记忆能力为12时,则他的识图能力为 .
若某儿童的记忆能力为12时,则他的识图能力为 .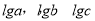 成等差数列
成等差数列 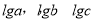 成等比数列
成等比数列 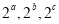 成等差数列
成等差数列