题目内容
 中,已知
中,已知 ,
, ,设
,设 ,
, 的周长为
的周长为 .
.
(Ⅰ)求 的表达式;(Ⅱ)当
的表达式;(Ⅱ)当 为何值时
为何值时 最大,并求出
最大,并求出 的最大值.
的最大值.
(Ⅰ)

 ,其中
,其中
(Ⅱ) 当 即
即 时,
时, 有最大值
有最大值
解析试题分析:(I) 中,根据正弦定理得:
中,根据正弦定理得:



 ,其中
,其中
(Ⅱ)

 +3
+3
= +3
+3
=
由 得
得
 当
当 即
即 时,
时, 有最大值
有最大值
考点:正弦定理 三角恒等变换
点评:本题主要考查两角和与差的三角函数公式,三角函数的图象与性质,解三角形等基础知识;考查运算求解能力,考查函数方程思想、数形结合思想.

练习册系列答案
相关题目
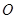 为圆心、
为圆心、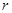 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心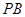 、西南方向上有一条一级公路
、西南方向上有一条一级公路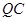 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆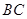 .已知通往一级公路的道路
.已知通往一级公路的道路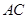 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是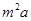 万元,其中
万元,其中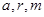 为常数,设
为常数,设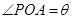 ,总造价为
,总造价为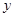 万元.
万元.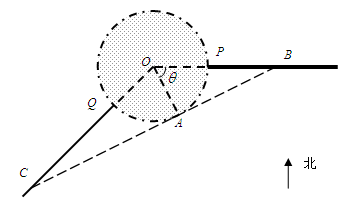
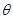 的函数
的函数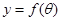 ,并求出定义域;
,并求出定义域;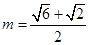 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低? ,解三角形ABC。
,解三角形ABC。 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
. 的大小;(2)若
的大小;(2)若 ,求
,求 的取值范围.
的取值范围. 的内角
的内角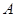 、
、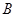 、
、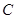 的对边分别为
的对边分别为 、
、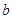 、
、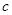 ,已知
,已知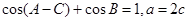 ,求
,求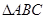 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是 、b、c,已知
、b、c,已知 ,且
,且 的夹角为
的夹角为 。
。 ,三角形的面积
,三角形的面积 ,求
,求 的值。
的值。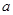 、
、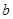 、
、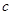 分别是
分别是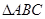 的三个内角
的三个内角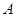 、
、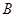 、
、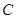 所对的边
所对的边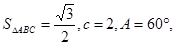 求
求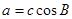 ,且
,且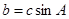 ,试判断
,试判断
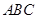 的内角
的内角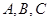 的对边分别为
的对边分别为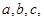
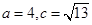 ,
,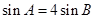 .
.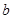 边的长; (2)求角
边的长; (2)求角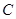 的大小。
的大小。