题目内容
如下图，函数y=2sin(πx＋φ),x∈R,(其中0≤φ≤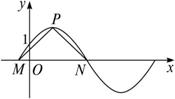
)的图象与y轴交于点（0，1）.
(1)求φ的值；
(2)设P是图象上的最高点，M、N是图象与x轴的交点，求
与
的夹角.
解：（1）因为函数图象过点（0，1），
所以2sin
=1,即sin=.因为0≤φ≤，所以
=
.
（2）由函数y=2sin(πx+
)及其图象，得M(-
,0),P(
,2),N(
,0)，
所以
=(-
,-2)，
=(
,-2)从而cos＜
，
＞=
，
故＜
,
＞=arccos
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知如图是函数y=2sin（ωx+φ）（|φ|＜
）的图象，那么（ ）
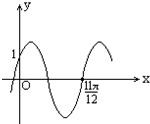
| π |
| 2 |
A、?=
| ||||
B、?=
| ||||
C、?=2，φ=
| ||||
D、?=2，φ=-
|
如图，函数y=2sin（πx+φ），x∈R，（其中0≤φ≤
如图，函数y=2sin（πx+φ），x∈R（其中0＜φ≤
)0≤
的图像与y轴交于点(0，1)．
与
夹角的余弦值．