题目内容
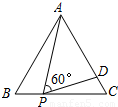
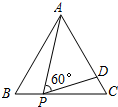
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( )
A.
| B.
| C.
| D.
|

∵△ABC是等边三角形,∴B=60°

在△ABP中,AB=3,BP=1,根据余弦定理,得
AP2=AB2+BP2-2AB•BPcosB=9+1-2×3×1×cos60°=7,可得AP=
根据正弦定理,得
=
,即
=
,解得sin∠APB=
∵△ABP中,AP2+BP2<AB2,得∠APB是钝角
∴cos∠APB=-
=-
△PCD中,∠CPD=180°-∠APB-∠APD=120°-∠APB
∴sin∠CPD=sin(120°-∠APB)=sin120°cos∠APB-cos120°sin∠APB=
×(-
)+
×
=
cos∠CPD=
=
因此,△PCD中,sin∠PDC=sin(∠CPD+∠C)=sin∠CPDcosC+cos∠CPDsinC=
×
+
×
=
由正弦定理,得
=
,
即
=
,解之得CD=
故选:B

在△ABP中,AB=3,BP=1,根据余弦定理,得
AP2=AB2+BP2-2AB•BPcosB=9+1-2×3×1×cos60°=7,可得AP=
| 7 |
根据正弦定理,得
| AB |
| sin∠APB |
| AP |
| sinB |
| 3 |
| sin∠APB |
| ||
| sin60° |
3
| ||
| 14 |
∵△ABP中,AP2+BP2<AB2,得∠APB是钝角
∴cos∠APB=-
| 1-sin2∠APB |
| ||
| 14 |
△PCD中,∠CPD=180°-∠APB-∠APD=120°-∠APB
∴sin∠CPD=sin(120°-∠APB)=sin120°cos∠APB-cos120°sin∠APB=
| ||
| 2 |
| ||
| 14 |
| 1 |
| 2 |
3
| ||
| 14 |
| ||
| 14 |
cos∠CPD=
| 1-sin2∠CPD |
5
| ||
| 14 |
因此,△PCD中,sin∠PDC=sin(∠CPD+∠C)=sin∠CPDcosC+cos∠CPDsinC=
| ||
| 14 |
| 1 |
| 2 |
5
| ||
| 14 |
| ||
| 2 |
3
| ||
| 14 |
由正弦定理,得
| PC |
| sin∠PDC |
| CD |
| sin∠CPD |
即
| 2 | ||||
|
| CD | ||||
|
| 2 |
| 3 |
故选:B

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
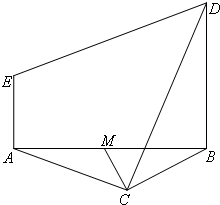 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点. 如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( )
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( ) 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.