题目内容
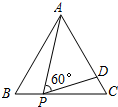
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( )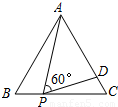
A.

B.

C.

D.

【答案】分析:在△ABP中,由余弦定理算出AP=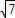 ,再用正弦定理算出sin∠APB=
,再用正弦定理算出sin∠APB=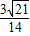 ,由同角三角函数的基本关系得cos∠APB=-
,由同角三角函数的基本关系得cos∠APB=-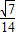 ,进而算出sin∠CPD=sin(120°-∠APB)=
,进而算出sin∠CPD=sin(120°-∠APB)=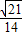 ,cos∠CPD=
,cos∠CPD=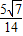 .然后在△PCD中算出sin∠PDC=sin(∠CPD+∠C)=
.然后在△PCD中算出sin∠PDC=sin(∠CPD+∠C)=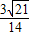 ,利用正弦定理列式,即可算出CD的长.
,利用正弦定理列式,即可算出CD的长.
解答:解:∵△ABC是等边三角形,∴B=60°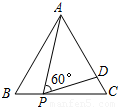
在△ABP中,AB=3,BP=1,根据余弦定理,得
AP2=AB2+BP2-2AB•BPcosB=9+1-2×3×1×cos60°=7,可得AP=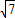
根据正弦定理,得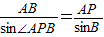 ,即
,即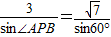 ,解得sin∠APB=
,解得sin∠APB=
∵△ABP中,AP2+BP2<AB2,得∠APB是钝角
∴cos∠APB=-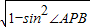 =-
=-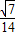
△PCD中,∠CPD=180°-∠APB-∠APD=120°-∠APB
∴sin∠CPD=sin(120°-∠APB)=sin120°cos∠APB-cos120°sin∠APB=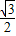 ×(-
×(-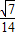 )+
)+ ×
×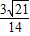 =
=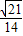
cos∠CPD=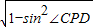 =
=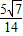
因此,△PCD中,sin∠PDC=sin(∠CPD+∠C)=sin∠CPDcosC+cos∠CPDsinC=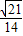 ×
× +
+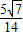 ×
×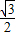 =
=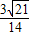
由正弦定理,得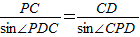 ,
,
即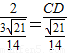 ,解之得CD=
,解之得CD=
故选:B
点评:本题给出边长为3的等边三角形ABC的边BC的一个三等分点P,在已知∠APD=60°的情况下求CD的长.着重考查了同角三角函数的基本关系、三角恒等变换和利用正余弦之理解三角形的知识,属于中档题.
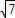 ,再用正弦定理算出sin∠APB=
,再用正弦定理算出sin∠APB=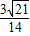 ,由同角三角函数的基本关系得cos∠APB=-
,由同角三角函数的基本关系得cos∠APB=-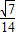 ,进而算出sin∠CPD=sin(120°-∠APB)=
,进而算出sin∠CPD=sin(120°-∠APB)=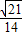 ,cos∠CPD=
,cos∠CPD=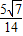 .然后在△PCD中算出sin∠PDC=sin(∠CPD+∠C)=
.然后在△PCD中算出sin∠PDC=sin(∠CPD+∠C)=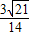 ,利用正弦定理列式,即可算出CD的长.
,利用正弦定理列式,即可算出CD的长.解答:解:∵△ABC是等边三角形,∴B=60°

在△ABP中,AB=3,BP=1,根据余弦定理,得
AP2=AB2+BP2-2AB•BPcosB=9+1-2×3×1×cos60°=7,可得AP=
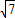
根据正弦定理,得
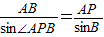 ,即
,即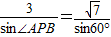 ,解得sin∠APB=
,解得sin∠APB=
∵△ABP中,AP2+BP2<AB2,得∠APB是钝角
∴cos∠APB=-
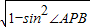 =-
=-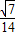
△PCD中,∠CPD=180°-∠APB-∠APD=120°-∠APB
∴sin∠CPD=sin(120°-∠APB)=sin120°cos∠APB-cos120°sin∠APB=
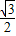 ×(-
×(-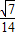 )+
)+ ×
×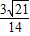 =
=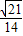
cos∠CPD=
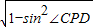 =
=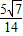
因此,△PCD中,sin∠PDC=sin(∠CPD+∠C)=sin∠CPDcosC+cos∠CPDsinC=
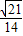 ×
× +
+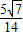 ×
×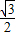 =
=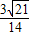
由正弦定理,得
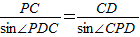 ,
,即
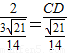 ,解之得CD=
,解之得CD=
故选:B
点评:本题给出边长为3的等边三角形ABC的边BC的一个三等分点P,在已知∠APD=60°的情况下求CD的长.着重考查了同角三角函数的基本关系、三角恒等变换和利用正余弦之理解三角形的知识,属于中档题.

练习册系列答案
相关题目
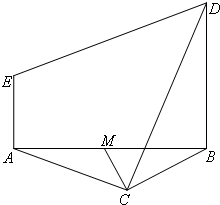 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点. 如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( )
如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为( ) 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.