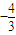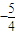题目内容
设函数 ,若f(x)在
,若f(x)在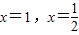 处取得极值.
处取得极值.(1)求a,b的值;
(2)存在
 使得不等式f(x)-c≤0成立,求c的最小值.
使得不等式f(x)-c≤0成立,求c的最小值.
【答案】分析:(1)由真数大于零求出函数的定义域,再求出函数的导数,由取得极值的必要条件得 ,列出方程组进行求解;
,列出方程组进行求解;
(2)由f(x)-c≤0成立,转化为c≥[f(x)]min,再由导数的符号确定函数在已知区间上的单调性,进而求出函数的极值,再求出区间端点处的函数值进行比较,求出函数的最小值.
解答:解:(1)∵ ,定义域为(0,+∞),
,定义域为(0,+∞),
∴ .…(1分),
.…(1分),
∵ 处取得极值,
处取得极值,
∴ …(2分)
…(2分)
即 ,解得
,解得 ,
,
∴所求的a,b的值分别为 …(4分)
…(4分)
(ii)因在 存在xo,使得不等式f(xo)-c≤0成立,
存在xo,使得不等式f(xo)-c≤0成立,
故只需c≥[f(x)]min,
由 =
= =
= .…(6分)
.…(6分)
f'(x)导数的符号如图所示
∴f(x)在区间 ,[1,2]递减;
,[1,2]递减;
 递增;…(7分)
递增;…(7分)
∴f(x)在区间 上的极小值是
上的极小值是 .…(8分)
.…(8分)
而 ,且
,且 ,
,
又∵e3-16>0,∴ …(10分)
…(10分)
∴[f(x)]min=f(2)…(11分)
∴ ,即c的最小值是
,即c的最小值是 …(12分)
…(12分)
点评:本题考查了利用函数的导数研究函数的单调性、极值和最值问题,以及恒成立转化问题,考查了分析及解决问题的能力.
 ,列出方程组进行求解;
,列出方程组进行求解;(2)由f(x)-c≤0成立,转化为c≥[f(x)]min,再由导数的符号确定函数在已知区间上的单调性,进而求出函数的极值,再求出区间端点处的函数值进行比较,求出函数的最小值.
解答:解:(1)∵
 ,定义域为(0,+∞),
,定义域为(0,+∞),∴
 .…(1分),
.…(1分),∵
 处取得极值,
处取得极值,∴
 …(2分)
…(2分)即
 ,解得
,解得 ,
,∴所求的a,b的值分别为
 …(4分)
…(4分)(ii)因在
 存在xo,使得不等式f(xo)-c≤0成立,
存在xo,使得不等式f(xo)-c≤0成立,故只需c≥[f(x)]min,
由
 =
= =
= .…(6分)
.…(6分)
f'(x)导数的符号如图所示
∴f(x)在区间
 ,[1,2]递减;
,[1,2]递减; 递增;…(7分)
递增;…(7分)∴f(x)在区间
 上的极小值是
上的极小值是 .…(8分)
.…(8分)而
 ,且
,且 ,
,又∵e3-16>0,∴
 …(10分)
…(10分)∴[f(x)]min=f(2)…(11分)
∴
 ,即c的最小值是
,即c的最小值是 …(12分)
…(12分)点评:本题考查了利用函数的导数研究函数的单调性、极值和最值问题,以及恒成立转化问题,考查了分析及解决问题的能力.

练习册系列答案
相关题目
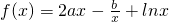 ,若f(x)在
,若f(x)在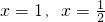 处取得极值.
处取得极值.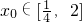 使得不等式f(x0)-c≤0成立,求c的最小值.
使得不等式f(x0)-c≤0成立,求c的最小值. ,若f(x)在
,若f(x)在 处取得极值.
处取得极值. 使得不等式f(x0)-c≤0成立,求c的最小值.
使得不等式f(x0)-c≤0成立,求c的最小值.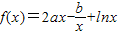 ,若f(x)在
,若f(x)在 处取得极值.
处取得极值.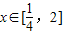 使得不等式f(x)-c≤0成立,求c的最小值.
使得不等式f(x)-c≤0成立,求c的最小值.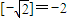 ,定义函数f(x)=x-[x].设函数
,定义函数f(x)=x-[x].设函数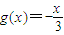 ,若f(x)在区间x∈(0,2)上零点的个数记为a,f(x)与g(x)图象交点的个数记为b,则
,若f(x)在区间x∈(0,2)上零点的个数记为a,f(x)与g(x)图象交点的个数记为b,则 的值是( )
的值是( )