题目内容
19.函数y=x|x+2|的单调减区间为(-2,-1).分析 根据所给的带有绝对值的函数式,讨论去掉绝对值,得到一个分段函数,利用二次函数的单调性即可得到减区间.
解答 解:当x>-2时,f(x)=x2+2x,
当x≤-2时,f(x)=-x2-2x,
这样就得到一个分段函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x>-2}\\{{-x}^{2}-2x,x≤-2}\end{array}\right.$.
f(x)=x2+2x的对称轴为:x=-1,开口向上,x>-2时是增函数;
f(x)=-x2-2x,开口向下,对称轴为x=-1,
则x<-1时函数是增函数,-2<x<-1时函数是减函数.
即有函数的单调减区间是[-2,-1].
故答案为:[-2,-1].
点评 本题考查二次函数的性质,本题解题的关键是去掉绝对值,把函数化成基本初等函数,可以通过函数的性质或者图象得到结果.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.复数z=$\frac{2i}{1-i}$(i是虚数单位),则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
4.四进制数1320(4)化为二进制数是( )
| A. | 111000 | B. | 1111000 | C. | 111200 | D. | 111100 |
11.直线l1、l2的斜率k1、k2是方程6x2+x-1=0的两根,则l1到l2的角是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{π}{2}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
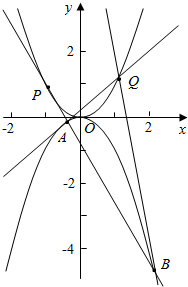 如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$
如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$ 已知正四面体A-BCD,棱长AD=2,则正四面体的外接球的体积为多少?
已知正四面体A-BCD,棱长AD=2,则正四面体的外接球的体积为多少?