题目内容
设f(x)=2x2+1,且a、b同号,a+b=1,证明对任意实数p、q恒有af(p)+bf(q)≥f(ap+bq)成立,并说明等号成立的条件.
证明:∵f(x)=2x2+1,
∴af(p)+bf(q)-f(ap+bq)=a(2p2+1)+b(2q2+1)-[2(ap+bq)2+1]
=2ap2+2bq2-2a2p2-4abpq-2b2q2+a+b-1.
又a+b=1,∴a+b-1=0.
∵af(p)+bf(q)-f(ap+bq)=2ap2-2a2p2+2bq2-2b2q2-4abpq
=2a(1-a)p2+2b(1-b)q2-4abpq=2abp2+2abq2-4abpq=2ab(p-q)2.
∵a、b同号,∴2ab(p-q)2≥0,当且仅当p=q时等号成立.
∴af(p)+bf(q)≥f(ap+bq),当且仅当p=q时等号成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
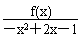 ≥-1的解集.
≥-1的解集.