题目内容
设f(x)=2x2+1,pq>0,p+q=1.求证:对任意实数a,b,恒有pf(a)+qf(b)≥f(pa+qb).
思路分析:通过作差变形得到2p(1-p)a2+2q(1-q)b2-4pqab+p+q-1,通过讨论,判断符号,发现证明思路,用综合法去证.
证明:考虑原式两边的差.
pf(a)+qf(b)-f(pa+qb)
=p(
=2p(1-p)a2+2q(1-q)b2-4pqab+p+q-1. ①
∵p+q=1,pq>0,
∴①式=2pqa2+2pqb2-4pqab
=2pq(a-b)2≥0.
即原式成立.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
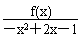 ≥-1的解集.
≥-1的解集.