题目内容
1.已知双曲线C:$\frac{{x}^{2}}{4}$-y2=1,P为C上的任意点.(1)设点A的坐标为(3,0),求|PA|的最小值
(2)求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数.
分析 (1)P(x,y),利用两点间的距离公式,结合消元法转化为一元二次函数形式进行求解即可.
(2)求出双曲线的渐近线,结合点到直线的距离公式进行求解.
解答 解:(1)设P(x,y),则$\frac{{x}^{2}}{4}$-1=y2,
则|PA|=$\sqrt{(x-3)^{2}+{y}^{2}}$=$\sqrt{\frac{5}{4}{x}^{2}-6x+8}$=$\sqrt{\frac{5}{4}(x-\frac{12}{5})^{2}+\frac{4}{5}}$
当x=$\frac{12}{5}$时,PA的最小值为$\sqrt{\frac{4}{5}}$=$\frac{2\sqrt{5}}{5}$,
(2)双曲线的渐近线:y=$±\frac{1}{2}$,设P(x,y),则$\frac{{x}^{2}}{4}$-y2=1,即$\frac{{x}^{2}-4{y}^{2}}{4}$=1.则x2-4y2=4,
P到两条渐近线的距离乘积$\frac{|x-2y|}{\sqrt{5}}•\frac{|x+2y|}{\sqrt{5}}$=$\frac{|{x}^{2}-4{y}^{2}|}{5}$=$\frac{4}{5}$为常数.
点评 本题主要考查双曲线的性质,设出点的坐标,利用点到直线的距离公式以及两点间的距离公式进行化简转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

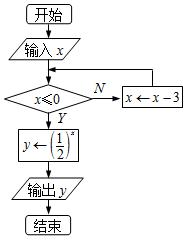 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.