题目内容
已知函数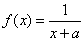 ,
,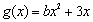 .
.
(Ⅰ)若曲线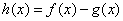 在点(1,0)处的切线斜率为0,求a,b的值;
在点(1,0)处的切线斜率为0,求a,b的值;
(Ⅱ)当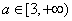 ,且ab=8时,求函数
,且ab=8时,求函数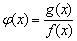 的单调区间,并求函数在区间[-2,-1]上的最小值。
的单调区间,并求函数在区间[-2,-1]上的最小值。
解:(Ⅰ)函数h(x)定义域为{x|x≠-a},
则 ,
,
 h(x)在点(1,0)处的切线斜率为0,
h(x)在点(1,0)处的切线斜率为0,

 即
即 ,解得
,解得 或
或
(Ⅱ)记 (x)=
(x)=  ,则
,则 (x)=(x+a)(bx2+3x)(x≠-a),
(x)=(x+a)(bx2+3x)(x≠-a),
 ab=8,所以
ab=8,所以 ,
,
 (x≠-a),
(x≠-a),

 ,
,
令 ,得
,得 ,或
,或 ,
,
 因为
因为 ,
, 所以
所以 ,
,
 故当
故当 ,或
,或 时,
时, ,当
,当 时,
时, ,
,
 函数
函数 (x)的单调递增区间为
(x)的单调递增区间为 ,
,
单调递减区间为 ,
,

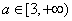 ,
,
 ,
, ,
,
当 ,即
,即 时,
时, 
 (x)在[-2,-1]单调递增,
(x)在[-2,-1]单调递增,

 (x)在该区间的最小值为
(x)在该区间的最小值为 ,
,
当 时,即
时,即 ,
,

 (x)在[-2,
(x)在[-2,
 单调递减, 在
单调递减, 在 单调递增,
单调递增,

 (x)在该区间的最小值为
(x)在该区间的最小值为

③当 时,即
时,即 时,
时,

 (x)在[-2,-1]单调递减,
(x)在[-2,-1]单调递减, 
 (x)在该区间的最小值为
(x)在该区间的最小值为 ,………13分
,………13分
综上所述,当 时,最小值为
时,最小值为 ;当
;当 时,最小值为
时,最小值为 ;当
;当 时,最小值为
时,最小值为 .
.

练习册系列答案
相关题目
为了稳定市场,确保农民增收,某农产品3月以后的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前六个月的市场收购价格:( )
则前七个月该产品的市场收购价格的方差为
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
A. B.
B. C.11 D.
C.11 D.
 为虚数单位,复数
为虚数单位,复数 的虚部是
的虚部是 B.
B. C.
C. D .
D . 
 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则 ( )
( ) 关于x的一元二次不等式
关于x的一元二次不等式 的解集中有且仅有3个整数,则所有符合条件的a的值之和是
的解集中有且仅有3个整数,则所有符合条件的a的值之和是
 ,则输出
,则输出 的值是
的值是
 是定义在
是定义在 上的单调递增函数,且
上的单调递增函数,且 时,
时, ,若
,若 ,则
,则 ;
;
 与圆
与圆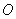 相切于
相切于 ,半径
,半径 ,
, 交
交 于
于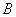 ,若
,若 ,
, ,则
,则 ,
, .
. 