题目内容
18.已知函数$f(x)=cos(2x+\frac{π}{3})+{sin^2}x$,则f(x)最小正周期为π.分析 利用三角恒等变换化简函数f(x),求出它的最小正周期即可.
解答 解:函数$f(x)=cos(2x+\frac{π}{3})+{sin^2}x$
=cos2xcos$\frac{π}{3}$-sin2xsin$\frac{π}{3}$+$\frac{1-cos2x}{2}$
=-$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$,
∴f(x)的最小正周期为:
T=$\frac{2π}{2}$=π.
故答案为:π.
点评 本题主要考查了三角函数的周期性及其求法,余弦函数的图象与性质,是基础题.

练习册系列答案
相关题目
14.下列叙述不正确的是( )
| A. | 类比推理是由特殊到特殊的推理 | |
| B. | 归纳推理是由特殊到一般的推理 | |
| C. | 演绎推理是由一般到特殊的推理 | |
| D. | 合情推理和演绎推理所得的结论都是正确的 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{-\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | (-∞,$\frac{1}{4}$) | B. | (2,+∞) | C. | (-2,$\frac{1}{4}$) | D. | (-∞,2)∪($\frac{1}{4}$,+∞) |
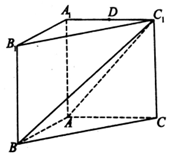 如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C
如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C