题目内容
如图,设M点是圆C:x2+(y-4)2=4上的动点,过点M作圆O:x2+y2=18的两条切线,切点分别为A,B,切线MA,MB分别交x轴于D,E两点。
(1)求四边形MAOB面积的最小值;
(2)是否存在点M,使得线段DE被圆C在点M处的切线平分?若存在,求出点M的纵坐标;若不存在,说明理由。
(1)求四边形MAOB面积的最小值;
(2)是否存在点M,使得线段DE被圆C在点M处的切线平分?若存在,求出点M的纵坐标;若不存在,说明理由。
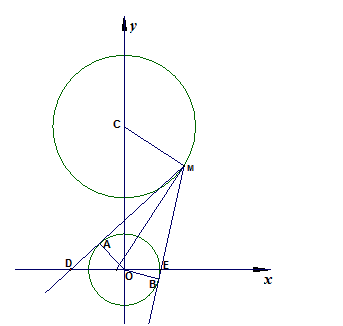
解:(1)面积最小值为 ;
;
(2)设存在点M(x0,y0)满足条件,
设过点M且与圆O相切的直线方程为: ,
,
则由题意得, ,化简得:
,化简得: ,
,
设直线MA,MB的斜率分别为k1,k2,则
圆C在点M处的切线方程为 ,
,
令y=0,得切线与x轴的交点坐标为 ,
,
又得D,E的坐标分别为 ,
,
由题意知,
用韦达定理代入可得, ,与
,与 联立,得
联立,得 。
。
 ;
;(2)设存在点M(x0,y0)满足条件,
设过点M且与圆O相切的直线方程为:
 ,
,则由题意得,
 ,化简得:
,化简得: ,
,设直线MA,MB的斜率分别为k1,k2,则

圆C在点M处的切线方程为
 ,
,令y=0,得切线与x轴的交点坐标为
 ,
,又得D,E的坐标分别为
 ,
,由题意知,

用韦达定理代入可得,
 ,与
,与 联立,得
联立,得 。
。 
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
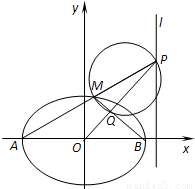
 如图,A,B是椭圆C:
如图,A,B是椭圆C: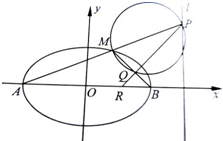 如图,A,B是椭圆
如图,A,B是椭圆 如图,A,B是椭圆C:
如图,A,B是椭圆C: 的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m.
的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m. ,m=4,求椭圆C的方程;
,m=4,求椭圆C的方程;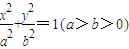 的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m.
的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m. ,m=4,求椭圆C的方程;
,m=4,求椭圆C的方程;