题目内容
如图,![]() 两点分别在射线OS、OT上移动,且
两点分别在射线OS、OT上移动,且![]() O为坐标原点,动点P满足
O为坐标原点,动点P满足![]()
(Ⅰ)求m?n的值;
(Ⅱ)求点P的轨迹C的方程,并说明它表示怎么样的曲线;
(Ⅲ)若直线l过点E(2,0)交(Ⅱ)中曲线C于M、N两点(M、N、E三点互不相同),且![]() 求l的方程.
求l的方程.

解:(Ⅰ)由已知得![]()
![]()
![]()
(Ⅱ)设P点坐标为(x,y)(x>0),由![]() 得
得
![]()
![]()
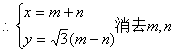 可得
可得
![]()
∴P点的轨迹方程为![]()
它表示以坐标原点为中心,焦点在x轴上,且实轴长为2,焦距为4的双曲线
![]() 的右支
的右支
(Ⅲ)设直线l的方程为![]() ,将其代入C的方程得
,将其代入C的方程得
![]()
即![]()
易知![]() (否则,直线l的斜率为
(否则,直线l的斜率为![]() ,它与渐近线平行,不符合题意)
,它与渐近线平行,不符合题意)
又△144t2-36![]()
设![]()
∵l与C的两个交点M,N在y轴右侧
![]()
![]()
![]()
![]()
![]() ,
,
又∵t=0不合题意
![]()
又由![]() 同理可得
同理可得
![]()
由![]()
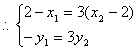
由![]()
由![]()
消去![]()
解之得:![]() ,满足
,满足![]()
故所求直线l存在,其方程为:![]()

练习册系列答案
相关题目
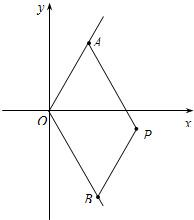 如图,
如图,
