已知正方体的外接球的体积是.则这个正方体的棱长是( )A． B． C． D．题目和参考答案——青夏教育精英家教网——

题目内容

已知正方体的外接球的体积是，则这个正方体的棱长是(　　)

A．

B．

C．

D．

D

解析试题分析：先求球的半径，直径就是正方体的对角线，然后求出正方体的棱长．
正方体外接球的体积是，则外接球的半径
正方体的对角线的长为2，棱长等于，
故选D．
考点：球内接多面体；球的体积和表面积．

练习册系列答案

小学暑假作业东南大学出版社系列答案

津桥教育暑假拔高衔接广东人民出版社系列答案

开拓者系列丛书新课标暑假作业大众文艺出版社系列答案

波波熊暑假作业江西人民出版社系列答案

快乐寒假假期作业云南教育出版社系列答案

金牌奥校暑假作业中国少年儿童出版社系列答案

快乐假期暑假电子科技大学出版社系列答案

学习报快乐暑假系列答案

暑假接力棒江苏凤凰少年儿童出版社系列答案

学而优暑期衔接南京大学出版社系列答案

相关题目

若两个球的表面积之比为,则这两个球的体积之比为（　　）

已知四面体ABCD中，AB＝AD＝6，AC＝4，CD＝2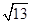，AB⊥平面ACD，则四面体 ABCD外接球的表面积为（）

已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为．直径为4的球的体积为，则（　　）

一个圆柱内接于一个底面半径为2，高为3的圆锥，如下图是圆锥的轴截面图，则内接圆柱侧面积最大值是（）

有一个长方体容器,装的水恰好占其容积的一半；表示水平的桌面,容器一边紧贴桌面，沿将其翻转使之倾斜，最后水面(阴影部分)与其各侧棱的交点分别是（如图），设翻转后容器中的水形成的几何体是，翻转过程中水和容器接触面积为,则下列说法正确的是（）

一个几何体的三视图如图所示，正视图和侧视图都是等边三角形，且该几何体的四个点在空间直角坐标系中构坐标分别是(0，0，0)，(2，0，0)，(2，2，0)，(0，2，0)，则第五个顶点的坐标可能为（）

A．（1，1，1）

一个空间几何体的三视图如图所示，该几何体的体积为则正视图中的值为（）

某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的表面积为( )