题目内容
已知椭圆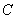 :
: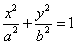
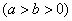 的两个焦点分别为
的两个焦点分别为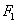 ,
,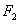 ,离心率为
,离心率为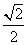 ,且过点
,且过点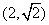 .
.
(Ⅰ)求椭圆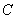 的标准方程;
的标准方程;
(Ⅱ)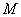 ,
,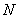 ,
,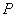 ,
,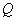 是椭圆
是椭圆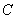 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和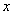 轴垂直的直线
轴垂直的直线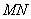 和
和 分别过点
分别过点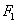 ,
,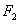 ,且这两条直线互相垂直,求证:
,且这两条直线互相垂直,求证: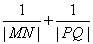 为定值.
为定值.
(Ⅰ)解:由已知 ,
,
所以 .
.
所以 .
.
所以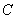 :
: ,即
,即 .
.
因为椭圆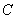 过点
过点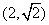 ,
,
得 ,
,  .
.
所以椭圆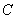 的方程为
的方程为 .
.
(Ⅱ)证明:由(Ⅰ)知椭圆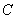 的焦点坐标为
的焦点坐标为 ,
, .
.
根据题意, 可设直线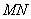 的方程为
的方程为 ,
,
由于直线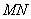 与直线
与直线 互相垂直,则直线
互相垂直,则直线 的方程为
的方程为 .
.
设 ,
, .
.
由方程组 消
消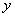 得
得
 .
.
则 
 .
.
所以
 =
= .
.
同理可得
 .
.
所以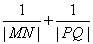


 .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
对于函数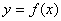 ,部分
,部分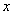 与
与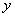 的对应关系如下表:
的对应关系如下表:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
数列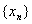 满足
满足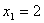 ,且对任意
,且对任意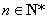 ,点
,点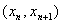 都在函数
都在函数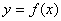 的图象上,则
的图象上,则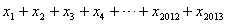 的值为
的值为
(A)9394 (B)9380 (C)9396 (D)9400
 C.19 D .21
C.19 D .21 为虚数单位,计算
为虚数单位,计算 .
. 
 , 则位于第10行的第8列的项
, 则位于第10行的第8列的项 等于 ,
等于 , 在图中位于 .(填第几行的第几列)
在图中位于 .(填第几行的第几列)
 的焦点坐标是_____________ 。
的焦点坐标是_____________ 。 上的函数
上的函数 的对称轴为
的对称轴为 ,且当
,且当 时,
时, .若函数
.若函数 (
( )上有零点,则
)上有零点,则 的值为
的值为 或
或 (B)
(B) (C)
(C) 或
或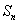 为等差数列
为等差数列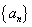 的前n项和.若
的前n项和.若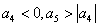 ,则使
,则使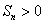 成立的最小正整数n为( )
成立的最小正整数n为( )