题目内容
已知两数列{an},{bn}(其中bn>0,且bn≠1),满足 且
且
(I)求证:an>bn
(II)求证:数列{an}的单调递减且 .
.
证明:(I)先证bn>1.∵bn>0,bn≠1,∴ =1,又
=1,又 ,∴bn>1.
,∴bn>1.
再证an>bn.① ;
;
②假设m=k时命题成立,即ak>bk>1,
则ak+1-bk+1= >
> =
= 0.
0.
∴ak+1>bk+1
所以n+k+1时命题也成立.
综合①②可得ak>bk.
(II)an+1-an= =
= ,
,
∵bn<an,∴ ,an>1,∴an+1-an<0.
,an>1,∴an+1-an<0.
故数列{an}单调递减.
∵
 ,
,
∴ …<
…< .
.
又a1-1=1,∴ ,
,
即 .
.
分析:(I)先证bn>1.由bn>0,bn≠1,利用基本不等式的性质即可得到 ;再利用数学归纳法证明an>bn即可;
;再利用数学归纳法证明an>bn即可;
(II)通过作差并利用(I)的结论即可证明单调性,再利用放缩法即可证明 .
.
点评:熟练掌握基本不等式的性质、数学归纳法、作差法、放缩法是解题的关键.注意利用已经证明的结论.
 =1,又
=1,又 ,∴bn>1.
,∴bn>1.再证an>bn.①
 ;
;②假设m=k时命题成立,即ak>bk>1,
则ak+1-bk+1=
 >
> =
= 0.
0.∴ak+1>bk+1
所以n+k+1时命题也成立.
综合①②可得ak>bk.
(II)an+1-an=
 =
= ,
,∵bn<an,∴
 ,an>1,∴an+1-an<0.
,an>1,∴an+1-an<0.故数列{an}单调递减.
∵

 ,
,∴
 …<
…< .
.又a1-1=1,∴
 ,
,即
 .
.分析:(I)先证bn>1.由bn>0,bn≠1,利用基本不等式的性质即可得到
 ;再利用数学归纳法证明an>bn即可;
;再利用数学归纳法证明an>bn即可;(II)通过作差并利用(I)的结论即可证明单调性,再利用放缩法即可证明
 .
.点评:熟练掌握基本不等式的性质、数学归纳法、作差法、放缩法是解题的关键.注意利用已经证明的结论.

练习册系列答案
相关题目
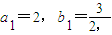 且
且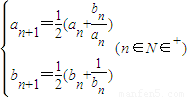
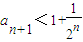 .
.