题目内容
已知两数列{an},{bn}(其中bn>0,且bn≠1),满足a1=2,b1=
且
(n∈N∈+)
(I)求证:an>bn
(II)求证:数列{an}的单调递减且an+1<1+
.
| 3 |
| 2, |
|
(I)求证:an>bn
(II)求证:数列{an}的单调递减且an+1<1+
| 1 |
| 2n |
证明:(I)先证bn>1.∵bn>0,bn≠1,∴bn+1=
(bn+
)>
×2
=1,又b1=
>1,∴bn>1.
再证an>bn.①a1=2,b1=
,a1>b1>1;
②假设m=k时命题成立,即ak>bk>1,
则ak+1-bk+1=
(ak+
)-
(bk+
)>
(ak+
)-
(bk+
)=
(ak+bk)(1-
)>0.
∴ak+1>bk+1
所以n+k+1时命题也成立.
综合①②可得ak>bk.
(II)an+1-an=
(an+
)-an=
(
-an),
∵bn<an,∴
<1,an>1,∴an+1-an<0.
故数列{an}单调递减.
∵an+1=
(an+
)<
(an+1),
∴an+1-1<
(an-1)<…<
(a1-1).
又a1-1=1,∴an+1-1<
,
即an+1<1+
.
| 1 |
| 2 |
| 1 |
| bn |
| 1 |
| 2 |
bn×
|
| 3 |
| 2 |
再证an>bn.①a1=2,b1=
| 3 |
| 2 |
②假设m=k时命题成立,即ak>bk>1,
则ak+1-bk+1=
| 1 |
| 2 |
| bk |
| ak |
| 1 |
| 2 |
| 1 |
| bk |
| 1 |
| 2 |
| 1 |
| ak |
| 1 |
| 2 |
| 1 |
| bk |
| 1 |
| 2 |
| 1 |
| akbk |
∴ak+1>bk+1
所以n+k+1时命题也成立.
综合①②可得ak>bk.
(II)an+1-an=
| 1 |
| 2 |
| bn |
| an |
| 1 |
| 2 |
| bn |
| an |
∵bn<an,∴
| bn |
| an |
故数列{an}单调递减.
∵an+1=
| 1 |
| 2 |
| bn |
| an |
| 1 |
| 2 |
∴an+1-1<
| 1 |
| 2 |
| 1 |
| 2n |
又a1-1=1,∴an+1-1<
| 1 |
| 2n |
即an+1<1+
| 1 |
| 2n |

练习册系列答案
相关题目
 且
且
 .
.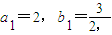 且
且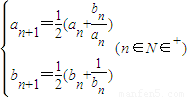
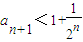 .
.