题目内容
【题目】已知函数
.
（1）若
时，讨论函数
的单调性；
（2）若函数在区间
上恰有2个零点，求实数
的取值范围.
【答案】（1）见解析；（2）
【解析】分析：（1）求出
，分三种情况讨论
的范围，在定义域内，分别令
求得
的范围，可得函数
增区间，
求得的范围，可得函数的减区间；（2）分三种情况讨论的范围，分别利用导数研究函数的单调性，结合零点存在定理与函数图象，可筛选出函数
在区间
上恰有2个零点的实数的取值范围.
详解：（1）
当
时，
，此时在
单调递增；
当
时，
①当
时，
，
恒成立，
，此时在单调递增；
②当
时，令
在
和
上单调递增；在
上单调递减；
综上：当
时，在单调递增；
当时，在和上单调递增；
在上单调递减；
（2）当时，由（1）知，在
单调递增，
，
此时在区间上有一个零点，不符；
当时，
，
在单调递增；，
此时在区间上有一个零点，不符；
当
时，要使在内恰有两个零点，必须满足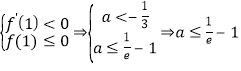
在区间上恰有两个零点时，
练习册系列答案
阅读快车系列答案
相关题目
