题目内容
设a为第四象限的角,若
=
,则tan2a=______.
| sin3a |
| sina |
| 13 |
| 5 |
∵a为第四象限的角∴sinα<0,cosα>0
∵
=
=
=2cos2α+cos2α=4cos2α-1=
∴cosα=
,sinα=-
tanα=-
tan2α=
=-
故答案为:-
∵
| sin3a |
| sina |
| sin(2α+α) |
| sinα |
| sin2αcosα+cos2αsinα |
| sinα |
| 13 |
| 5 |
∴cosα=
3
| ||
| 10 |
| ||
| 10 |
tanα=-
| 1 |
| 3 |
| 2tanα |
| 1-tan2α |
| 3 |
| 4 |
故答案为:-
| 3 |
| 4 |

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
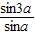 =
=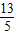 ,则tan2a= .
,则tan2a= .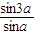 =
=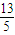 ,则tan2a= .
,则tan2a= .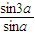 =
=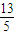 ,则tan2a= .
,则tan2a= .