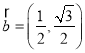题目内容
【题目】已知定义域为![]() 的单调函数
的单调函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)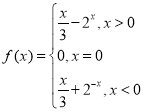 ;(2)
;(2)![]()
【解析】
(1)![]() 时利用
时利用![]() 可求
可求![]() 的解析式,再利用奇偶性考虑
的解析式,再利用奇偶性考虑![]() 与
与![]() 的关系,即可求出
的关系,即可求出![]() 时的解析式,要注意
时的解析式,要注意![]() 时的情况;
时的情况;
(2)先分析单调性,因为题设已告诉函数单调,故取值直接比较即可;然后利用![]() 是奇函数对不等式进行变形,转变为两个函数值的大小关系,根据单调性可去掉函数符号变为自变量间的大小关系,最后化为关于
是奇函数对不等式进行变形,转变为两个函数值的大小关系,根据单调性可去掉函数符号变为自变量间的大小关系,最后化为关于![]() 的不等式恒成立的问题去处理.
的不等式恒成立的问题去处理.
(1) 当![]() 时,
时, ![]() ,
,
∴![]() ,
,
又函数![]() 是奇函数,
是奇函数,
∴![]() ,
,
∴![]() .
.
又![]() .
.
综上所述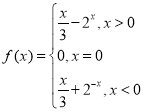 .
.
(2)∵![]() 为
为![]() 上的单调函数,且
上的单调函数,且![]() ,
,
∴函数![]() 在
在![]() 上单调递减.
上单调递减.
∵![]() ,
,
∴![]() ,
,
∵函数![]() 是奇函数,
是奇函数,
∴![]() .
.
又![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,
,
解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目