题目内容
4.函数f(x)=sin(-2x+$\frac{3π}{4}$)的单调增区间为[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$],k∈Z,单调减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.分析 由条件利用诱导公式、正弦函数的单调性,得出结论.
解答 解:∵函数f(x)=sin(-2x+$\frac{3π}{4}$)=-sin(2x-$\frac{3π}{4}$),
令2kπ-$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,
可得该函数的单调减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
令2kπ+$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{5π}{8}$≤x≤kπ+$\frac{9π}{8}$,
可得该函数的单调增区间为[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$],k∈Z.
故答案为:[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$],k∈Z;[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
点评 本题主要考查诱导公式、正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
19.执行如图所示的程序框图,若输入t的值为5,则输出的s的值为( )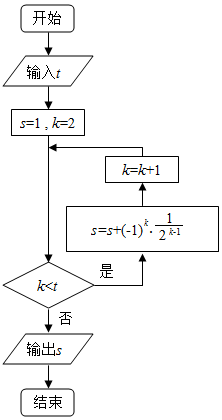

| A. | $\frac{9}{16}$ | B. | $\frac{5}{4}$ | C. | $\frac{21}{16}$ | D. | $\frac{11}{8}$ |
9.若函数y=$\frac{{2{{sin}^2}x+sin\frac{3x}{2}-4}}{{{{sin}^2}x+2{{cos}^2}x}}$既存在最大值M,又存在最小值m,则M+m的值为( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
16.已知ω>0,|φ|<$\frac{π}{2}$,若x=$\frac{π}{6}$和x=$\frac{7π}{6}$是函数f(x)=cos(ωx+φ)的两个相邻的极值点,将y=f(x)的图象向左平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则下列说法正确的是( )
| A. | y=g(x)是奇函数 | B. | y=g(x)的图象关于点(-$\frac{π}{2}$,0)对称 | ||
| C. | y=g(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=g(x)的周期为π |
14.已知角α的终边过点P(-4,-6sin150°),则sin2α的值为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
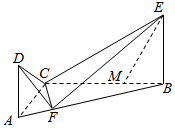 如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.
如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.