题目内容
10.已知正△ABC的边长为1,那么在斜二侧画法中它的直观图△A′B′C′的面积为$\frac{{\sqrt{6}}}{16}$.分析 由直观图和原图的面积之间的关系,直接求解即可.
解答 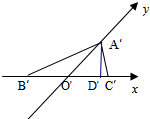 解:正三角形的高OA=$\frac{\sqrt{3}}{2}$,底BC=1,
解:正三角形的高OA=$\frac{\sqrt{3}}{2}$,底BC=1,
在斜二侧画法中,B′C′=BC=1,0′A′=$\frac{1}{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
则△A′B′C′的高A′D′=0′A′sin45°=$\frac{\sqrt{3}}{4}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{8}$,
则△A′B′C′的面积为S=$\frac{1}{2}B′C′•A′D′=\frac{1}{2}$×1×$\frac{\sqrt{6}}{8}$=$\frac{{\sqrt{6}}}{16}$,
故答案为:$\frac{{\sqrt{6}}}{16}$.
点评 本题考查斜二测画法中原图和直观图面积之间的关系,属基本运算的考查

练习册系列答案
相关题目
5.已知函数$f(x)=\left\{\begin{array}{l}(a-3)x+2,x≤1\\{x^{1-a}},x>1\end{array}\right.$是(-∞,+∞)上的减函数,那么a的取值范围是( )
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (2,3) |
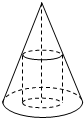 如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.
如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.