在复平面内.复数Z=$\frac{2}{3-i}+{i^3}$对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限题目和参考答案——青夏教育精英家教网—

题目内容

14．在复平面内，复数Z=$\frac{2}{3-i}+{i^3}$对应的点位于（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

分析利用复数代数形式的乘除运算化简，求出Z的坐标得答案．

解答解：复数Z=$\frac{2}{3-i}+{i^3}=\frac{{2（{3+i}）}}{{（{3-i}）（{3+i}）}}-i=\frac{3+i}{5}-i=\frac{3}{5}-\frac{4}{5}i$，
对应的点的坐标为（$\frac{3}{5}，-\frac{4}{5}$），位于第四象限．
故选：D．

点评本题考查复数代数形式的混合运算，考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案

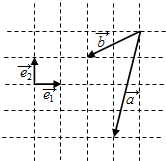
$-4\overrightarrow{e_1}-2\overrightarrow{e_2}$

B．

$-2\overrightarrow{e_1}-4\overrightarrow{e_2}$

C．

$\overrightarrow{e_1}-3\overrightarrow{e_2}$

D．

$3\overrightarrow{e_1}-\overrightarrow{e_2}$

5．命题“?x∈R，e^x-x＞0”的否定为?x∈R，e^x-x≤0．

2．已知抛物线C：y²=8x的焦点F与双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点重合，C的准线与E交于A，B，若|$\overrightarrow{AB}$|=6，则E的方程为x²-$\frac{{y}^{2}}{3}$=1．

9．设不等式组$\left\{\begin{array}{l}{x-y-1≤0}\\{x≥0}\\{y≤1}\end{array}\right.$表示的平面区域为M，则M的面积是2，目标函数z=x+y的最大值是3．

19．对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（单位：m/s）的数据如下：

甲	27	37	29	36	33	30
乙	32	28	37	33	27	35

（1）画出茎叶图；
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、极差、方差，并判断选谁参加比赛比较合适？

6．已知A、B、C是△ABC的内角，向量$\overrightarrow{m}$=（-1，$\sqrt{3}$），$\overrightarrow{n}$=（cosA，sinA），且$\overrightarrow{m}$•$\overrightarrow{n}$=1．
（1）求角A的大小；
（2）若$\frac{1+sin2B}{co{s}^{2}B-si{n}^{2}B}$=-2，求tanC．

3．已知F是抛物线y²=x的焦点，过F的直线l交抛物线与A，B两点，且|AB|=3，则线段AB的中点到y轴的距离为$\frac{5}{4}$．

4．

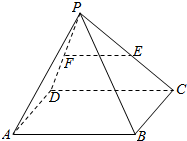如图所示，P是平行四边形ABCD外一点，E，F分别是PC，PD的中点，判断EF与平面PAB是否平行？

试题分类