题目内容
12.函数f(x)=$\left\{\begin{array}{l}{x^2}+x+1(x>0)\\ a+1(x=0)\\ b{x^2}+x+c(x<0)\end{array}$为奇函数,则a+b+c=-3.分析 由题意,f(0)=a+1=0,求出a=-1.f(-1)=-f(1),可得b-1+c=-(1+1+1),求出b+c=-2,即可得出结论.
解答 解:由题意,f(0)=a+1=0,∴a=-1.
f(-1)=-f(1),可得b-1+c=-(1+1+1),∴b+c=-2,
∴a+b+c=-3.
故答案为:-3.
点评 本题考查分段函数,考查函数的奇偶性,考查学生的计算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
2.下列各组函数中,表示同一个函数的是( )
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=|x| | B. | f(x)=x0,g(x)=1 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x+1}$,g(x)=x-1 | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
20.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x02-x0+1≤0,则¬P:?x∈R,x2-x+1>0 | |
| C. | 命题 P:若x=2且y=3,则x+y-5=0,命题P的否命题为假 | |
| D. | 设集合$A=\left\{{\left.x\right|\frac{x-1}{x+1}<0}\right\}$,B={x||x-1|<a},则“a=1”是“A∩B≠∅”的必要不充分条件 |
1.4名男歌手和2名女歌手联合举行一场音乐会,出场顺序要求两名女歌手不相邻,共有出场方案的种数是( )
| A. | $A_4^4A_5^2$ | B. | $A_4^4A_3^2$ | C. | $A_4^4A_2^2$ | D. | $A_4^4A_4^1A_3^1$ |
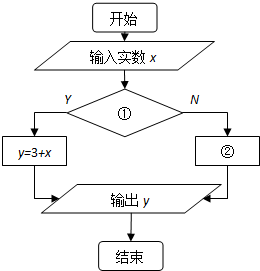 已知函数y=|x+3|,向量程序框表示的是给出x值,求所对应的函数值的算法,请将该程序框图补充完整,其中①处应填x≥-3;②处应填y=-x-3.
已知函数y=|x+3|,向量程序框表示的是给出x值,求所对应的函数值的算法,请将该程序框图补充完整,其中①处应填x≥-3;②处应填y=-x-3.