题目内容
已知函数![]() ,其中
,其中![]() 为大于零的常数.
为大于零的常数.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)求证:对于任意的![]() 且
且![]() 时,都有
时,都有![]() 成立.
成立.
解:![]() ……………2分
……………2分
(1)由已知,得![]() 在
在![]() 上恒成立, 即
上恒成立, 即![]() 在
在![]() 上恒成立
上恒成立
又当![]() 时,
时,![]() ,
,![]() ,即
,即![]() 的取值范围为
的取值范围为![]() ……………4分
……………4分
(2)当![]() 时,
时,![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
这时![]() 在[1,2]上为增函数,
在[1,2]上为增函数,![]()
当![]() ,
,![]() 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时![]() 在[1,2]上为减函数,
在[1,2]上为减函数,
![]()
当![]() 时,令
时,令![]() ,得
,得![]()
又![]() 对于
对于![]() 有
有![]() ,对于
,对于![]() 有
有![]() ,
,
![]() ……………7分
……………7分
综上,![]() 在[1,2]上的最小值为:
在[1,2]上的最小值为:
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]()
③当![]() 时,
时,![]() . ………9分
. ………9分
(3)由(1),知函数![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,
,![]() ,
,
即![]() ,对于
,对于![]() 恒成立,
恒成立,
![]()
![]()
![]() 对于
对于![]() ,且
,且![]() 时,
时,![]() 恒成立.………………14分
恒成立.………………14分

练习册系列答案
相关题目
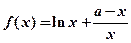 ,其中
,其中 为大于零的常数.
为大于零的常数.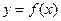 在点(1,
在点(1,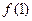 )处的切线与直线
)处的切线与直线 平行,求
平行,求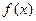 在区间[1,2]上的最小值.
在区间[1,2]上的最小值. ,其中
,其中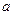 为大于零的常数.
为大于零的常数. 在点(1,
在点(1,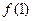 )处的切线与直线
)处的切线与直线 平行,求
平行,求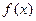 在区间[1,2]上的最小值.
在区间[1,2]上的最小值. (其中ω为大于0的常数),若函数
(其中ω为大于0的常数),若函数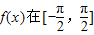 上是增函数,则ω的取值范围是 .
上是增函数,则ω的取值范围是 . ,其中
,其中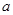 为大于零的常数.[来源:学科网]
为大于零的常数.[来源:学科网]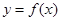 在点(1,
在点(1,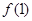 )处的切线与直线
)处的切线与直线 平行,求
平行,求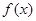 在区间[1,2]上的最小值.
在区间[1,2]上的最小值. ,其中
,其中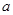 为大于零的常数.
为大于零的常数.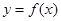 在点(1,
在点(1,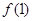 )处的切线与直线
)处的切线与直线 平行,求
平行,求 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.