题目内容
已知函数
（其中ω为大于0的常数），若函数
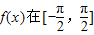上是增函数，则ω的取值范围是 ．
【答案】分析：根据两角和与差的正弦公式，可将函数f（x）的解析式化为f（x）=2sin（ωx+
）的形式，进而根据ω为大于0的常数，函数
上是增函数，可得
ω+
≤
，解不等式可得ω的取值范围．
解答：解：函数
=
+
+cosωx
=
sinωx+cosωx
=2sin（ωx+
）
由ω＞0且函数
上是增函数，
可得
ω+
≤
解得ω≤
故ω的取值范围是
故答案为：
点评：本题考查的知识点是两角和与差的正弦函数，熟练掌握两角和与差的正弦公式，对解析式进行化简是解答的关键．
）的形式，进而根据ω为大于0的常数，函数上是增函数，可得ω+≤，解不等式可得ω的取值范围．解答：解：函数
=
++cosωx=
sinωx+cosωx=2sin（ωx+
）由ω＞0且函数
上是增函数，可得
ω+≤解得ω≤
故ω的取值范围是
故答案为：
点评：本题考查的知识点是两角和与差的正弦函数，熟练掌握两角和与差的正弦公式，对解析式进行化简是解答的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
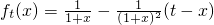，其中t为常数，且t＞0．
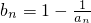，证明：对任意的x＞0，
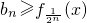，n=1，2，…．
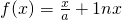，其中a为常数，e为自然对数的底数．
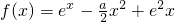，其中e为自然对数的底数，a∈R．
，其中
，
为自然对数的底数．
的单调性；
上的最大值．
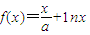，其中a为常数，e为自然对数的底数．