题目内容
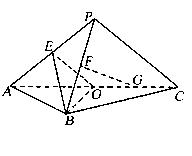
如图,平面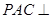 平面
平面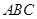 ,
,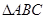 是以
是以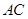 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,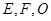 分别为
分别为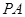 ,
,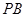 ,
,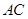 的中点,
的中点,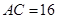 ,
,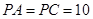 .
.
(1)设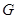 是
是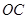 的中点,证明:
的中点,证明: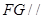 平面
平面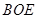 ;
;
(2)证明:在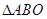 内存在一点
内存在一点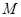 ,使
,使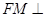 平面
平面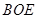 ,并求点
,并求点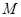 到
到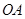 ,
,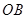 的距离.
的距离.
(1)详见解析, (2) 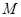 到
到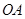 ,
,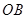 的距离为
的距离为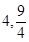 .
.
解析试题分析:(1) 证明线面平行,关键在于找出线线线平行.本题中点较多,易从中位线上找平行.取线段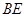
中点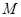 ,连接
,连接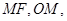 则
则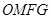 所以为平行四边形,因此
所以为平行四边形,因此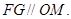 运用线面平行判定定理时,需写
运用线面平行判定定理时,需写
全定理所需所有条件.(2) 在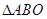 内找一点,利用空间向量解决较易. 利用平面
内找一点,利用空间向量解决较易. 利用平面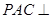 平面
平面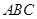 ,建立空间直角坐标系O
,建立空间直角坐标系O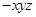 ,点M的坐标可设为
,点M的坐标可设为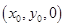 .利用
.利用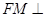 平面
平面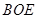 ,可解出
,可解出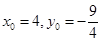 ,但需验证点M满足
,但需验证点M满足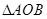 的内部区域,再由点M的坐标得点
的内部区域,再由点M的坐标得点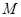 到
到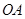 ,
,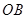 的距离为
的距离为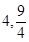 .
.
试题解析:证明:(1)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为 轴,
轴,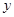 轴,
轴,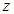 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O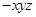 , 则
, 则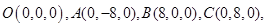
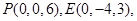
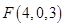 ,由题意得,
,由题意得,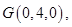 因
因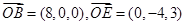 ,因此平面BOE的法向量
,因此平面BOE的法向量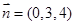 ,
,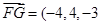 得
得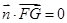 ,又直线
,又直线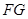 不在平面
不在平面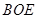 内,因此有
内,因此有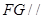 平面
平面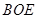 6分
6分
(2)设点M的坐标为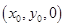 ,则
,则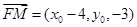 ,因为
,因为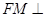 平面BOE,所以有
平面BOE,所以有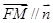 ,因此有
,因此有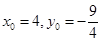 ,即点M的坐标为
,即点M的坐标为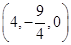 ,在平面直角坐标系
,在平面直角坐标系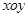 中,
中,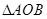 的内部区域满足不等式组
的内部区域满足不等式组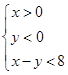 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在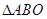 内存在一点
内存在一点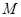 ,使
,使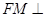 平面
平面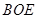 ,由点M的坐标得点
,由点M的坐标得点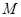 到
到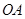 ,
,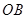 的距离为
的距离为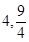 . 12分
. 12分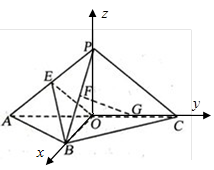
考点:线面平行判定定理,空间向量研究线面垂直

练习册系列答案
相关题目
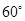 ,∠BAC
,∠BAC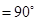 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC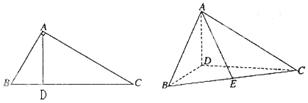
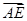 与
与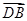 夹角的余弦值.
夹角的余弦值.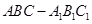 中,侧棱
中,侧棱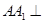 平面
平面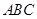 ,
, 为等腰直角三角形,
为等腰直角三角形,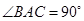 ,且
,且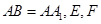 分别是
分别是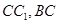 的中点.
的中点.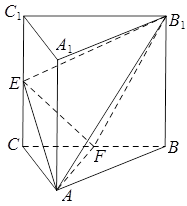
 平面
平面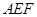 ;
;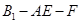 的余弦值.
的余弦值.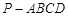 的底面为直角梯形,
的底面为直角梯形,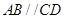 ,
,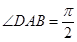 ,
,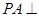 底面
底面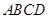 ,且
,且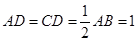 ,
,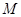 是
是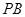 的中点.
的中点.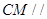 平面
平面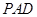 ;
; 与平面
与平面 所成的角为
所成的角为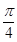 ,求二面角
,求二面角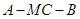 的余弦值.
的余弦值.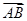 ,b=
,b=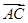 .
.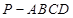 中,
中,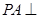 面
面 ,
,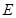 、
、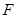 分别为
分别为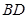 、
、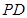 的中点,
的中点, ,
,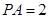 .
.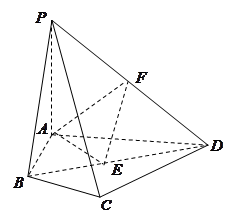
 ∥面
∥面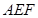 ;
;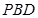 与面
与面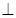 底面ABCD,且SA=2,AD=DC=1
底面ABCD,且SA=2,AD=DC=1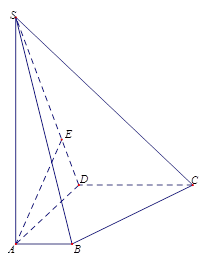
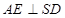 证明:
证明: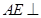 平面
平面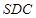 ;
;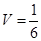 ,求面SAD与面SBC所成二面角的正弦值的大小
,求面SAD与面SBC所成二面角的正弦值的大小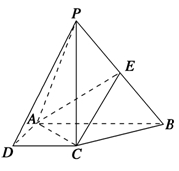
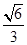 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.