题目内容
16.已知数列{an}(n∈N*,1≤n≤46)满足a1=a,an+1-an=$\left\{{\begin{array}{l}{d,1≤n≤15}\\{1,16≤n≤30}\\{\frac{1}{d},31≤n≤45}\end{array}}$其中d≠0,n∈N*.(1)当a=1时,求a46关于d的表达式,并求a46的取值范围;
(2)设集合M={b|b=ai+aj+ak,i,j,k∈N*,1≤i<j<k≤16}.若a=$\frac{1}{3}$,d=$\frac{1}{4}$,求证:2∈M.
分析 (1)根据数列的递推关系,进行递推即可,求a46关于d的表达式,并求a46的取值范围;
(2)根据数列的递推关系求出b的表达式,即可证明结论.
解答 解:(1)当a=1时,a16=1+15d,a31=16+15d,${a_{46}}=16+15(d+\frac{1}{d})$.
因为d≠0,$d+\frac{1}{d}≥2$,或$d+\frac{1}{d}≤-2$,
所以a46∈(-∞,-14]∪[46,+∞).
(2)由题意${a_n}=\frac{1}{3}+\frac{n-1}{4}$,1≤n≤16,$b=1+\frac{i+j+k-3}{4}$.
令$1+\frac{i+j+k-3}{4}=2$,得i+j+k=7.
因为i,j,k∈N*,1≤i<j<k≤16,
所以令i=1,j=2,k=4,则2∈M.
点评 本题主要考查递推数列的应用,考查学生运算和推理能力,有一定的难度.

练习册系列答案
相关题目
4.已知x、y∈R,不等式组$\left\{\begin{array}{l}x+2y≥0\\ x-y≤0\\ 0≤y≤k\end{array}\right.$所表示的平面区域的面积为6,则实数k的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.执行如图所示的算法流程图.若输入x=0,则输出的y的值是( )
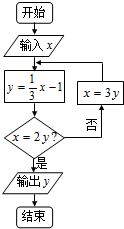

| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
 如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=1,∠BAP=120°,则圆O的面积为π.
如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=1,∠BAP=120°,则圆O的面积为π.