题目内容
设函数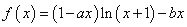 ,其中
,其中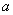 和
和 是实数,曲线
是实数,曲线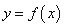 恒与
恒与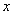 轴相切于坐标原点.
轴相切于坐标原点.
(1)求常数 的值;
的值;
(2)当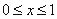 时,关于
时,关于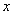 的不等式
的不等式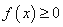 恒成立,求实数
恒成立,求实数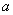 的取值范围;
的取值范围;
(3)求证:对于任意的正整数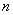 ,不等式
,不等式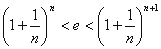 恒成立.
恒成立.
解:(1) 对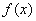 求导得:
求导得: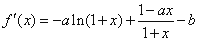 ,根据条件知
,根据条件知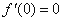 ,所以
,所以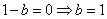 . ……………2分
. ……………2分
(2) 由(1)得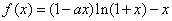 ,
,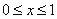
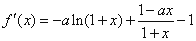
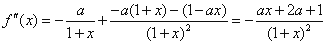 .
.
① 当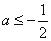 时,由于
时,由于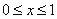 ,有
,有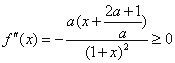 ,于是
,于是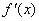 在
在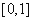 上单调递增,从而
上单调递增,从而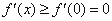 ,因此
,因此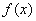 在
在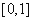 上单调递增,即
上单调递增,即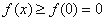 而且仅有
而且仅有 ;
;
②当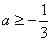 时,由于
时,由于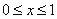 ,有
,有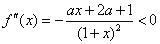 ,于是
,于是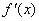 在
在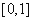 上单调递减,从而
上单调递减,从而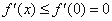 ,因此
,因此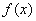 在
在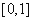 上单调递减,即
上单调递减,即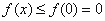 而且仅有
而且仅有 ;
;
③当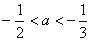 时,令
时,令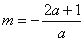 ,当
,当 时,
时,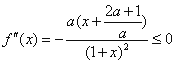 ,于是
,于是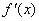 在
在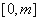 上单调递减,从而
上单调递减,从而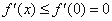 ,因此
,因此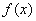 在
在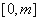 上单调递减,[]
上单调递减,[]
即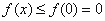 而且仅有
而且仅有 .
.
综上可知,所求实数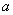 的取值范围是
的取值范围是 . ……………8分
. ……………8分
(3) 对要证明的不等式等价变形如下:
对于任意的正整数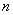 ,不等式
,不等式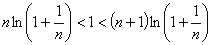 恒成立. 并且继续作如下等价变形
恒成立. 并且继续作如下等价变形
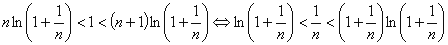
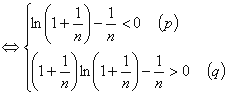
对于 相当于(2)中
相当于(2)中 ,情形,有
,情形,有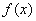 在
在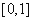 上单调递减,即
上单调递减,即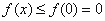 而且仅有
而且仅有 .
.
取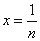 ,得:对于任意正整数
,得:对于任意正整数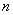 都有
都有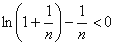 成立;
成立;
对于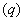 相当于(2)中
相当于(2)中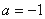 情形,对于任意
情形,对于任意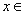
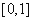 ,恒有
,恒有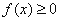 而且仅有
而且仅有 .
.
取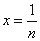 ,得:对于任意正整数
,得:对于任意正整数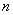 都有
都有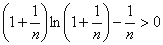 成立.
成立.
因此对于任意正整数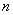 ,不等式
,不等式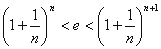 恒成立
恒成立

练习册系列答案
相关题目
 的虚部为 .
的虚部为 . 中,
中, ,
, ,
, 是
是 的个位数字,
的个位数字, 是
是 的前
的前 项和,则
项和,则 .
. 在区间
在区间 上的导函数为
上的导函数为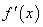 ,
, ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数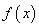 在区间
在区间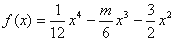 在
在 上为“凸函数”,则实数m的取值范围是
上为“凸函数”,则实数m的取值范围是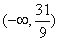 B.
B.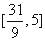 C.
C. D.
D.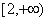
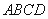
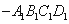 的表面上运动,且
的表面上运动,且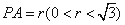 ,记点P的轨迹长度为
,记点P的轨迹长度为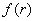 .给出以下四个命题:
.给出以下四个命题: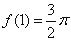 ;
; 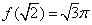 ;
; 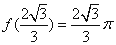
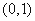 上是增函数,
上是增函数,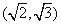 上是减函数。
上是减函数。 +
+ =1,则x+y的最小值是( )
=1,则x+y的最小值是( ) (C)
(C) (D)
(D) 
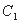 的参数方程为
的参数方程为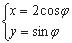 (
( 为参数),以
为参数),以 为极点,
为极点,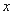 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线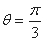 与曲线
与曲线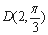
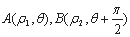 是曲线
是曲线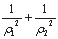 的值;
的值;