题目内容
5．求证：2a4-a2≥2a3-1．分析 利用作差法证明不等式即可．
解答 证明：2a4+1-2a3-a2
=2a3（a-1）-（a-1）（a+1）
=（a-1）（2a3-a-1）
=（a-1）（a-1）（2a2+2a+1）
=（a-1）2（2a2+2a+1），
∵（a-1）2≥0；
2a2+2a+1＞0 （其判别式小于0）
所以，（a-1）2（2a2+2a+1）≥0
即2a4-a2≥2a3-1．
点评 本题考查不等式的证明，考查计算能力以及逻辑推理能力．
练习册系列答案
相关题目
20．
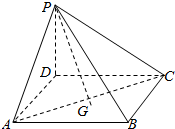如图，在四棱锥P-ABCD中，PD⊥底面ABCD，ABCD为正方形，且PD=AB=1，G为△ABC的重心，则PG与底面所成的角θ满足（ ）
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，ABCD为正方形，且PD=AB=1，G为△ABC的重心，则PG与底面所成的角θ满足（ ）| A． | θ=$\frac{π}{4}$ | B． | cosθ=$\frac{2\sqrt{34}}{17}$ | C． | tanθ=$\frac{2\sqrt{2}}{3}$ | D． | sinθ=$\frac{\sqrt{3}}{3}$ |
