题目内容
13.已知函数f(x)=2sin(x+$\frac{π}{2}$)•sin(x+$\frac{7π}{3}$)-$\sqrt{3}$sin2x+sin(π+x)cos(x+3π).(1)求函数f(x)的单调递增区间及对称轴方程;
(2)若B为△ABC的内角,且满足f($\frac{B}{2}$)=$\sqrt{3}$,求∠B.
分析 化简得出函数关系式f(x)=2sin(2x+$\frac{π}{3}$).
(1)根据正弦函数的单调性得出$-\frac{π}{2}$+2kπ≤2x$+\frac{π}{3}$≤$\frac{π}{2}$+2kπ,求解即可得出单调区间.
利用2x$+\frac{π}{3}$=$kπ+\frac{π}{2}$,k∈z,可求对称轴
(2)代入函数关系式得出2sin(B+$\frac{π}{3}$)=$\sqrt{3}$,0<B<π,求解即可.
解答 解:∵函数f(x)=2sin(x+$\frac{π}{2}$)•sin(x+$\frac{7π}{3}$)-$\sqrt{3}$sin2x+sin(π+x)cos(x+3π).
∴f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=sinxcosx+$\sqrt{3}$cos2x-$\sqrt{3}$sin2x+sinxcosx
=$\sqrt{3}$cos2x+sin2x
=2sin(2x+$\frac{π}{3}$)
(1)∵$-\frac{π}{2}$+2kπ≤2x$+\frac{π}{3}$≤$\frac{π}{2}$+2kπ,
即$-\frac{5π}{12}$+kπ≤x≤kπ$+\frac{π}{12}$,k∈z,
∴函数f(x)的单调递增区间为:[$-\frac{5π}{12}$+kπ,kπ$+\frac{π}{12}$],k∈z,
∵2x$+\frac{π}{3}$=$kπ+\frac{π}{2}$,k∈z,
∴x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈z.
∴对称轴方程为:x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈z.
(2)∵B为△ABC的内角,且满足f($\frac{B}{2}$)=$\sqrt{3}$,
∴2sin(B+$\frac{π}{3}$)=$\sqrt{3}$,0<B<π
即∠B=$\frac{π}{3}$.
点评 本题考察了三角函数的图象性质,化简运算,解三角形,属于三角部分的综合题目,属于中档题.

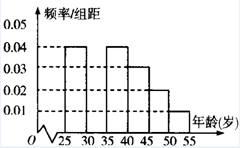 某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行
某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行了一次有关“房地产投资”的调查,得到如下统计数据和频率分布直方图:
| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | P |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
(Ⅱ)从年龄在[40,50)岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,并从中选取3人作为代表发言,记选取的3名代表中年龄在
[40,45)岁的人数为X,求X的分布列和数学期望.