题目内容
设a为实常数,y=f(x)是定义在R上的奇函数,当x<0时,f(x)=9x+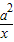 +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
【答案】分析:先利用y=f(x)是定义在R上的奇函数求出x≥0时函数的解析式,将f(x)≥a+1对一切x≥0成立转化为函数的最小值≥a+1,利用基本不等式求出f(x)的最小值,解不等式求出a的范围.
解答:解:因为y=f(x)是定义在R上的奇函数,
所以当x=0时,f(x)=0;
当x>0时,则-x<0,所以f(-x)=-9x-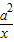 +7
+7
因为y=f(x)是定义在R上的奇函数,
所以f(x)=9x+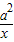 -7;
-7;
因为f(x)≥a+1对一切x≥0成立,
所以当x=0时,0≥a+1成立,
所以a≤-1;
当x>0时,9x+ -7≥a+1成立,
-7≥a+1成立,
只需要9x+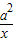 -7的最小值≥a+1,
-7的最小值≥a+1,
因为9x+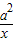 -7≥2
-7≥2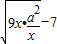 =6|a|-7,
=6|a|-7,
所以6|a|-7≥a+1,
解得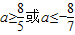 ,
,
所以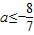 .
.
故答案为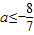 .
.
.
点评:本题考查函数解析式的求法;考查解决不等式恒成立转化成求函数的最值;利用基本不等式求函数的最值.
解答:解:因为y=f(x)是定义在R上的奇函数,
所以当x=0时,f(x)=0;
当x>0时,则-x<0,所以f(-x)=-9x-
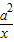 +7
+7因为y=f(x)是定义在R上的奇函数,
所以f(x)=9x+
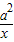 -7;
-7;因为f(x)≥a+1对一切x≥0成立,
所以当x=0时,0≥a+1成立,
所以a≤-1;
当x>0时,9x+
 -7≥a+1成立,
-7≥a+1成立,只需要9x+
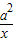 -7的最小值≥a+1,
-7的最小值≥a+1,因为9x+
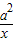 -7≥2
-7≥2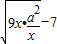 =6|a|-7,
=6|a|-7,所以6|a|-7≥a+1,
解得
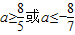 ,
,所以
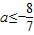 .
.故答案为
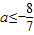 .
..
点评:本题考查函数解析式的求法;考查解决不等式恒成立转化成求函数的最值;利用基本不等式求函数的最值.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
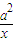 +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .