题目内容
函数设a为实常数,y=f(x)是定义在R上的奇函数,当x<0时,f(x)=4x+
+9,若f(x)≥a+1对一切x≥0恒成立,则a的取值范围为
| a2 | x |
(-∞,-2]
(-∞,-2]
.分析:利用奇函数的性质可得:当x>0时,f(x)=-f(-x)=4x+
-9.当x>0时,化为4x2-(a+10)x+a2≥0在x>0时恒成立.
令g(x)=4x2-(a+10)x+a2,转化为
,或△=(a+10)2-16a2≤0.当x=0时,比较简单.
| a2 |
| x |
令g(x)=4x2-(a+10)x+a2,转化为
|
解答:解:设x>0,则-x<0,∴f(-x)=-4x-
+9.
由于f(x)≥a+1对一切x≥0恒成立,
(1)当x>0时,f(x)=-f(-x)=4x+
-9,∴4x+
-9≥a+1恒成立,
化为4x2-(a+10)x+a2≥0在x>0时恒成立.
令g(x)=4x2-(a+10)x+a2,
利用二次函数的图象与性质可得两种情况:①对称轴在y轴的左侧或是y轴
,或②图象不在x轴的下方,则△=(a+10)2-16a2≤0,
解得①a≤-10.②a≤-2或a≥
.
(2)当x=0时,f(0)=0≥a+1恒成立,解得a≤-1.
综上可知:(-∞,-2].
| a2 |
| x |
由于f(x)≥a+1对一切x≥0恒成立,
(1)当x>0时,f(x)=-f(-x)=4x+
| a2 |
| x |
| a2 |
| x |
化为4x2-(a+10)x+a2≥0在x>0时恒成立.
令g(x)=4x2-(a+10)x+a2,
利用二次函数的图象与性质可得两种情况:①对称轴在y轴的左侧或是y轴
|
解得①a≤-10.②a≤-2或a≥
| 10 |
| 3 |
(2)当x=0时,f(0)=0≥a+1恒成立,解得a≤-1.
综上可知:(-∞,-2].
点评:熟练掌握奇函数的性质和二次函数的图象与△的关系是解题的关键.

练习册系列答案
相关题目
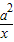 +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .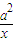 +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .