题目内容

a为何值时，方程ax2+2x+1=0至少有一个负实根.

解：（1）当a=0时，2x+1=0，x=-，有一个负实根.

（2）当a≠0时，若x=0，则原方程为1=0，无意义，因此方程若有实根，必为：①两正根；②一正一负；③两负根.若考虑“②一正一负；③两负根”，则需分两种情况讨论，若仅考虑“①两正根”则问题显得很简单，只要取“①两正根”的补集即可.

由Δ=4-4a≥0得{a|a≤1}，这就是本题中的全集.

若ax2+2x+1=0（a≠0)有两正根，则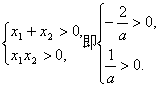这样的a不存在，这说明只要{a|a≤1}，方程ax2+2x+1=0的两根必为“②一正一负；③两负根.”综上得：a≤1.

练习册系列答案
相关题目
已知，圆C：x2+y2-8y+12=0，直线l：ax+y+2a=0．
（1）当a为何值时，直线l与圆C相切；
（2）当直线l与圆C相交于A、B两点，且AB=2
2
时，求直线l的方程．
已知双曲线的一条渐近线方程为y=
3
x，且其中一个焦点坐标为(
2
3
3
，0)
（1）求双曲线的方程．
（2）若直线y-ax-1=0与该双曲线交于A、B两点，当a为何值时，A、B在双曲线的同一支上？
（1）已知一个圆经过点P（5，1），且圆心在点C（6，-2），求圆的方程．
（2）已知圆C：x2+y2-8y+12=0，直线l：ax+y+2a=0．求当a为何值时，直线l与圆C相切．

设关于x的方程2x2－ax－2=0的两根为α、β(α＜β),函数f(x)=. 

(1)求f(α)·f(β)的值；

(2)证明f(x)是［α，β］上的增函数；

(3)当a为何值时，f(x)在区间［α，β］上的最大值与最小值之差最小？

已知：圆C：x2＋y2－8y＋12＝0，直线l：ax＋y＋2a＝0.

(1)当a为何值时，直线l与圆C相切；

(2)当直线l与圆C相交于A、B两点，且AB＝2时，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网